题目内容
1.如图1,已知在平行四边形ABCD中,AB=10,BC=16,sinB=$\frac{3}{5}$,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.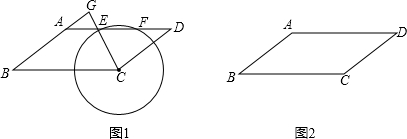
(1)当圆C经过点A时,求CP的长;
(2)联结AP,当AP∥CG时,求弦EF的长;
(3)当△AGE是等腰三角形时,求CG的长.
分析 (1)当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,直接利用勾股定理求出AC进而得出答案;
(2)首先得出四边形APCE是菱形,进而得出CM的长,进而利用锐角三角函数关系得出CP以及EF的长;
(3)∠GAE≠∠BGC,只能∠AGE=∠AEG,利用AD∥BC,得出△GAE∽△GBC,进而求出CG的长.
解答 解:(1)如图1,设⊙O的半径为r,
当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,
∵sinB=$\frac{3}{5}$,
∴cosB=$\frac{4}{5}$
∴BH=AB•cosB=8,
∴AH=AB•sinB=6,
CH=BC-BH=8,
∴AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=10,
∴此时CP=CA=r=10;
(2)如图2 ,
,
若AP∥CE,APCE为平行四边形,
∵CE=CP,
∴四边形APCE是菱形,
连接AC、EP,则AC⊥EP,
∴AM=CM=$\frac{1}{2}$CA=5,
由(1)知,AB=AC,
则∠ACB=∠B,
∴CP=CE=$\frac{CM}{cos∠ACB}$=$\frac{25}{4}$,
过C作CN⊥EF于N
则EF=2EN=2$\sqrt{C{E}^{2}-C{N}^{2}}$=$\frac{7}{2}$;
(3)如图3,
∵cosB=$\frac{4}{5}$,
∴∠B<45°,
∵∠BCG<90°,
∴∠BGC>45°,
∵∠AEG=∠BCG≥∠GAE=∠B,
∴当∠AEG=∠GAE时,∠BCG=∠B,A、E、G重合,
∴只能∠AGE=∠AEG,
∵AD∥BC,
∴△GAE∽△GBC,
∴$\frac{AE}{CB}=\frac{AG}{BG}$,
∴$\frac{CB}{BG}=\frac{AE}{AG}=1$,
即BC=BG=AB+AG,
16=10+AG,
∴AG=6=AE,
过G作GQ⊥AE于Q,
则GQ=AGsin∠GAE=6×$\frac{3}{5}$$\frac{18}{5}$,
AQ=AGcos∠GAE=6×$\frac{4}{5}$=$\frac{24}{5}$,
EQ=AE-AQ=6-$\frac{24}{5}$=$\frac{6}{5}$,
∴GE=$\sqrt{E{Q}^{2}+G{Q}^{2}}$,
=$\frac{6}{5}\sqrt{10}$,
又由△GAE∽△GBC,得$\frac{GC}{GE}=\frac{BC}{AE}$,
即$\frac{\frac{CG}{6\sqrt{10}}}{5}=\frac{16}{6}$,
∴CG=$\frac{16\sqrt{10}}{5}$.
点评 此题主要考查了相似三角形的判定与性质以及勾股定理以及锐角三角函数关系等知识,利用分类讨论得出△AGE是等腰三角形时只能∠AGE=∠AEG进而求出是解题关键.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案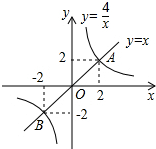 正比例函数y=x与反比例函数y=$\frac{4}{x}$的图象交于A(2,2)、B(-2,-2)两点,当x>$\frac{4}{x}$时,x的取值范围是( )
正比例函数y=x与反比例函数y=$\frac{4}{x}$的图象交于A(2,2)、B(-2,-2)两点,当x>$\frac{4}{x}$时,x的取值范围是( )| A. | -2<x<0或x>2 | B. | -2<x<0或0<x<2 | C. | x>2 | D. | x<-2 |
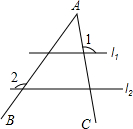 如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )
如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 45° |
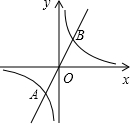 如图,已知正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点为A(-1,2-k2),另一个交点为B,且A,B关于原点O对称.
如图,已知正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点为A(-1,2-k2),另一个交点为B,且A,B关于原点O对称.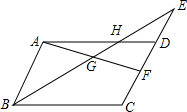 如图,在?ABCD中,DH=$\frac{1}{2}$AH,点F是边CD的中点,
如图,在?ABCD中,DH=$\frac{1}{2}$AH,点F是边CD的中点,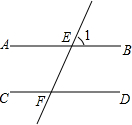 已知,直线AB、CD被EF所截,∠AEF=∠EFD,求证:AB∥CD.
已知,直线AB、CD被EF所截,∠AEF=∠EFD,求证:AB∥CD.