题目内容
9.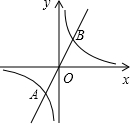 如图,已知正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点为A(-1,2-k2),另一个交点为B,且A,B关于原点O对称.
如图,已知正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点为A(-1,2-k2),另一个交点为B,且A,B关于原点O对称.(1)求反比例函数和正比例函数的解析式;
(2)请直接写出关于x的不等式$\frac{k}{x}$-ax>0的解集.
分析 (1)把A的坐标代入反比例函数解析式求出k的值,即可得出反比例函数解析式和A的坐标,把A的坐标代入正比例函数解析式求出即可;
(2)根据A、B的坐标和图象即可得出不等式的解集.
解答 解:(1)由图知k>0,a>0,
∵点A(-1,2-k2)在y=$\frac{k}{x}$图象上,
∴2-k2=-k,即 k2-k-2=0,
解得 k1=2,k2=-1(舍去),
即反比例函数解析式为:y=$\frac{2}{x}$,
将x=-1,y=$\frac{2}{-1}$=-2,代入y=ax,解得:a=2,
∴正比例函数解析式为:y=2x;
(2)关于x的不等式$\frac{k}{x}$-ax>0的解集为x<-1或0<x<1.
点评 本题考查了一次函数和反比例函数的交点问题,用待定系数法求函数的解析式,函数的图象的应用,解此题的关键是能求出两函数的解析式,数形结合思想的应用,难度适中.

练习册系列答案
相关题目
19.下列各数中无理数是( )
| A. | $\frac{7}{11}$ | B. | -1 | C. | 0 | D. | $\frac{π}{3}$ |
17.因式分解x3-4x的结果是( )
| A. | x(x2-4) | B. | x(x-4)2 | C. | x(x-2)(x+2) | D. | x(x-2)2 |
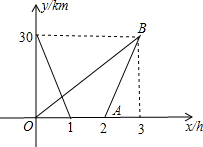 小强开车、小斌骑自行车分别同时从各自的家中出发,匀速相向而行,小强在到达小斌家后停留1h,原路返回自己家,小斌一直匀速骑电动车3h后,与小强同时到达小强家,如图表示两人距小斌家的距离y(km)与时间x(h)之间的函数关系
小强开车、小斌骑自行车分别同时从各自的家中出发,匀速相向而行,小强在到达小斌家后停留1h,原路返回自己家,小斌一直匀速骑电动车3h后,与小强同时到达小强家,如图表示两人距小斌家的距离y(km)与时间x(h)之间的函数关系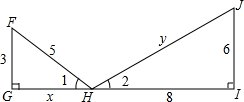 根据图中所注的条件,判断图中两个三角形是否相似,并求出x的值.
根据图中所注的条件,判断图中两个三角形是否相似,并求出x的值.
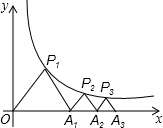 如图,点P1(x1,y1)、P2(x2,y2)、P3(x3,y3)、…、Pn(xn,yn)、Pn+1(xn+1、yn+1)(n为正整数)在反比例函数y=$\frac{8}{x}$(x>0)的图象像上,且x1=2,xn+1=xn+2,分别连接OP1、OP2、OP3、…、OPn、OPn+1;构成若干个三角形,记△P1OP2的面积为S1,△P2OP3的面积为S2,…,依此类推,则Sn=$\frac{16n-8}{n(n-1)}$(用含有n的代数式表示)
如图,点P1(x1,y1)、P2(x2,y2)、P3(x3,y3)、…、Pn(xn,yn)、Pn+1(xn+1、yn+1)(n为正整数)在反比例函数y=$\frac{8}{x}$(x>0)的图象像上,且x1=2,xn+1=xn+2,分别连接OP1、OP2、OP3、…、OPn、OPn+1;构成若干个三角形,记△P1OP2的面积为S1,△P2OP3的面积为S2,…,依此类推,则Sn=$\frac{16n-8}{n(n-1)}$(用含有n的代数式表示)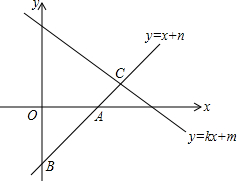 如图,直线AB的解析式为y=x+n与直线y=kx+m交于C点(其中k,m,n为常数)点C的横坐标为3,下列四个结论:
如图,直线AB的解析式为y=x+n与直线y=kx+m交于C点(其中k,m,n为常数)点C的横坐标为3,下列四个结论: