题目内容
15.在平面直角坐标系中,直线y1=$\frac{1}{3}$x+a和y2=-$\frac{1}{4}$x+b交于点E(3,3),点P(m,n)在直线y1=$\frac{1}{3}$x+a上,过点P(m,n)作x轴的垂线,交直线y2=-$\frac{1}{4}$x+b于点F.(1)若n=2,求△PEF的面积;
(2)若PF=2,求点P的坐标.
分析 (1)根据直线y1=$\frac{1}{3}x$+a和直线y2=-$\frac{1}{4}x$+b的交点为E(3,3)求得a=2,b=$\frac{15}{4}$,得到直线y1=$\frac{1}{3}x+2$和直线y2=-$\frac{1}{4}x+\frac{15}{4}$,求得P(0,2),即可得到结果;
(2)由(1)知,点P在y1=$\frac{1}{3}x$+2,点F在y2=-$\frac{1}{4}x+\frac{15}{4}$,由于PF⊥x轴,可设P(m,$\frac{1}{3}m+2$),F(m,-$\frac{1}{4}m+\frac{15}{4}$),于是得到PF=|($\frac{1}{3}m+2$)-(-$\frac{1}{4}m+\frac{15}{4}$)|=2即可得到结果.
解答 (1)解:∵直线y1=$\frac{1}{3}x$+a和直线y2=-$\frac{1}{4}x$+b的交点为E(3,3)
∴3=$\frac{1}{3}$×3+a,3=-$\frac{1}{4}$×3+b,
∴a=2,b=$\frac{15}{4}$,
得直线y1=$\frac{1}{3}x+2$和直线y2=-$\frac{1}{4}x+\frac{15}{4}$,如图所示,
又∵n=2,∴2=$\frac{1}{3}m+2$,m=0,
∴P(0,2),
过点P(0,2)作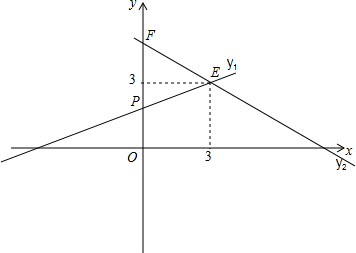 x轴的垂线,交y2=-$\frac{1}{4}x+\frac{15}{4}$直线于点F,
x轴的垂线,交y2=-$\frac{1}{4}x+\frac{15}{4}$直线于点F,
F(0,$\frac{15}{4}$),
∴PF=$\frac{7}{4}$,
∴${S}_{△PEF}=\frac{1}{2}×\frac{7}{4}×3=\frac{21}{8}$,
(2)解:由(1)知,点P在y1=$\frac{1}{3}x$+2,点F在y2=-$\frac{1}{4}x+\frac{15}{4}$,
∵PF⊥x轴,可设P(m,$\frac{1}{3}m+2$),F(m,-$\frac{1}{4}m+\frac{15}{4}$),
∴PF=|($\frac{1}{3}m+2$)-(-$\frac{1}{4}m+\frac{15}{4}$)|=2,
∴m=-$\frac{3}{7}$或m=$\frac{45}{7}$,
∴P(-$\frac{3}{7}$,$\frac{13}{7}$)或P($\frac{45}{7}$,$\frac{29}{7}$).
点评 本题考查了两直线相交或平行的问题,一次函数的性质,三角形的面积的求法,求点的坐标,正确的理解题意是解题的关键.

| A. | (-8,-3) | B. | (-2,-2) | C. | (2,5) | D. | (-6,-1) |
 已知,如图,梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,E点是腰AB上的一点,联结CE.
已知,如图,梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,E点是腰AB上的一点,联结CE.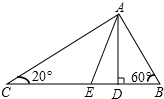 如图,在△ABC中,∠B=60°,∠C=20°,AD为△ABC的高,AE为角平分线.求∠EAD的度数.
如图,在△ABC中,∠B=60°,∠C=20°,AD为△ABC的高,AE为角平分线.求∠EAD的度数.
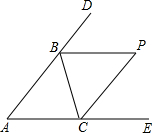 如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.
如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.