题目内容
阅读,如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有x1+x2=-
,x1x2=
.这是一元二次方程根与系数的关系,我们可以用它来解题.应用:已知x1,x2是方程2x2-6x-1=0的两根,则(x1-x2)2的值为 .
| b |
| a |
| c |
| a |
考点:根与系数的关系
专题:
分析:先根据根与系数的关系得到x1+x2=3,x1x2=-
,再利用完全平方公式变形得到(x1-x2)2=(x1+x2)2-4x1x2,然后利用整体代入的方法计算即可.
| 1 |
| 2 |
解答:解:根据题意得x1+x2=-
=3,x1x2=
=-
,
所以(x1-x2)2=(x1+x2)2-4x1x2=32-4×(-
)=11.
故答案为11.
| -6 |
| 2 |
| -1 |
| 2 |
| 1 |
| 2 |
所以(x1-x2)2=(x1+x2)2-4x1x2=32-4×(-
| 1 |
| 2 |
故答案为11.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
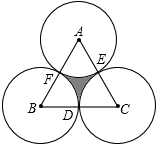 如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为
如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为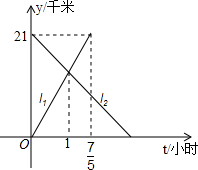 甲乙两人分别从相距21千米的A,B两地同时出发,相向而行,如图,l1,l2分别表示甲乙两人距A地的距离y(千米)与时间t(小时)之间的关系
甲乙两人分别从相距21千米的A,B两地同时出发,相向而行,如图,l1,l2分别表示甲乙两人距A地的距离y(千米)与时间t(小时)之间的关系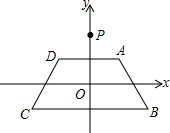 如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )
如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )