题目内容
 如图,AD平分∠BAC,BD⊥AD,DE∥AC,求证:△BDE是等腰三角形.
如图,AD平分∠BAC,BD⊥AD,DE∥AC,求证:△BDE是等腰三角形.考点:等腰三角形的判定
专题:证明题
分析:由AD平分∠BAC,得出∠EAD=∠CAD,DE∥AC,得出∠CAD=∠ADE,进一步得出∠EAD=∠ADE,再进一步利用等角的余角相等得出∠BDE=∠B,证得结论.
解答:证明:∵AD平分∠BAC,
∴∠EAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠EAD=∠ADE,
∵BD⊥AD
∴∠ADE+∠BDE=90°,
∴∠EAD+∠B=90°,
∴∠BDE=∠B,
∴BE=DE,
∴△BDE是等腰三角形.
∴∠EAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠EAD=∠ADE,
∵BD⊥AD
∴∠ADE+∠BDE=90°,
∴∠EAD+∠B=90°,
∴∠BDE=∠B,
∴BE=DE,
∴△BDE是等腰三角形.
点评:此题考查等腰三角形的判定,角平分线的性质,平行线的性质,等角的余角相等等知识,注意条件与结论之间的联系.

练习册系列答案
相关题目
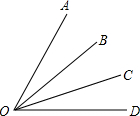 如图,射线OB、OC将∠AOD分成三部分,下列判断错误的是( )
如图,射线OB、OC将∠AOD分成三部分,下列判断错误的是( )| A、如果∠AOB=∠COD,那么∠AOC=∠BOD |
| B、如果∠AOB>∠COD,那么∠AOC>∠BOD |
| C、如果∠AOB<∠COD,那么∠AOC<∠BOD |
| D、如果∠AOB=∠BOC,那么∠AOC=∠BOD |
 如图,点B位于点O的南偏西45°方向上,∠AOB=70°,则点A位于O的( )
如图,点B位于点O的南偏西45°方向上,∠AOB=70°,则点A位于O的( )| A、北偏西65° |
| B、西偏北35° |
| C、南偏北25° |
| D、东偏北45° |
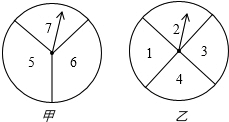 如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字.
如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字.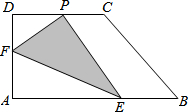 如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.AE=5,P落在线段CD上时,PD=
如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.AE=5,P落在线段CD上时,PD=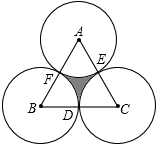 如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为
如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为 如图,∠AOB=90°,OB是∠COD的平分线,OE为CO的延长线.
如图,∠AOB=90°,OB是∠COD的平分线,OE为CO的延长线.