题目内容
 如图,已知抛物线y=
如图,已知抛物线y=| 1 |
| 7 |
(1)求点P的坐标;
(2)求抛物线的解析式.
考点:抛物线与x轴的交点
专题:
分析:(1)在等腰直角△AMP中,MA=MP,则利用AB=4、BM:PM=7:3来求点P的坐标;
(2)根据点P的坐标易求点A的坐标,把点A、P的坐标分别代入函数解析式求得系数的值即可.
(2)根据点P的坐标易求点A的坐标,把点A、P的坐标分别代入函数解析式求得系数的值即可.
解答: 解:(1)如图,∵∠PAB=135°,
解:(1)如图,∵∠PAB=135°,
∴∠MAP=45°,
∴∠MPA=∠MAP=45°,
∴MP=MA.
又∵BM:PM=7:3,AB=4,
∴(4+MP):PM=7:3,则MP=3.
∵点P的横坐标为-1,
∴点P的坐标为:(-1,-3);
(2)由(1)知,点P的坐标为(-1,-3),MP=MA=3.
则OA=3-1=2.
故A(2,0),
所以 把点A、P的坐标分别代入函数y=
x2+bx+c,得
,
解得
.
故该二次函数解析式为:y=
x2+
x-
.
 解:(1)如图,∵∠PAB=135°,
解:(1)如图,∵∠PAB=135°,∴∠MAP=45°,
∴∠MPA=∠MAP=45°,
∴MP=MA.
又∵BM:PM=7:3,AB=4,
∴(4+MP):PM=7:3,则MP=3.
∵点P的横坐标为-1,
∴点P的坐标为:(-1,-3);
(2)由(1)知,点P的坐标为(-1,-3),MP=MA=3.
则OA=3-1=2.
故A(2,0),
所以 把点A、P的坐标分别代入函数y=
| 1 |
| 7 |
|
解得
|
故该二次函数解析式为:y=
| 1 |
| 7 |
| 6 |
| 7 |
| 16 |
| 7 |
点评:本题考查了抛物线与x轴的交点坐标.根据已知条件推知△MPA是等腰直角三角形是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 图中,同旁内角的对数为( )
图中,同旁内角的对数为( )| A、14 | B、16 | C、18 | D、20 |
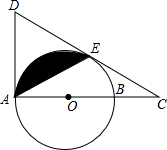 如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.
如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.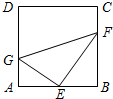 如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )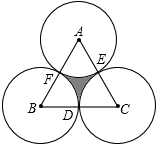 如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为
如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为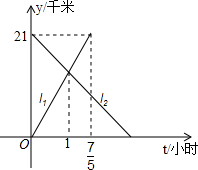 甲乙两人分别从相距21千米的A,B两地同时出发,相向而行,如图,l1,l2分别表示甲乙两人距A地的距离y(千米)与时间t(小时)之间的关系
甲乙两人分别从相距21千米的A,B两地同时出发,相向而行,如图,l1,l2分别表示甲乙两人距A地的距离y(千米)与时间t(小时)之间的关系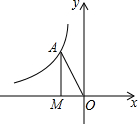 如图,若点A在反比例函数y=
如图,若点A在反比例函数y=