题目内容
如图，四边形ABCD是矩形，四边形AECF是菱形，若AB=4，BC=8，求菱形AECF的面积．考点：菱形的性质,矩形的性质
专题：
分析：由四边形AECF是菱形，可得AE=EC，由四边形ABCD是矩形，可得∠B=90°，然后设AE=EC=x，则BE=BC-EC=8-x，可得方程：42+（8-x）2=x2，继而求得菱形AECF的面积．
解答：解：∵四边形AECF是菱形，
∴AE=EC，
设AE=EC=x，则BE=BC-EC=8-x，
∵四边形ABCD是矩形，
∴∠B=90°，
∴AB2+BE2=AE2，
∵AB=4，
∴42+（8-x）2=x2，
解得：x=5，
∴EC=5，
∴S菱形AECF=EC•AB=5×4=20．
∴AE=EC，
设AE=EC=x，则BE=BC-EC=8-x，
∵四边形ABCD是矩形，
∴∠B=90°，
∴AB2+BE2=AE2，
∵AB=4，
∴42+（8-x）2=x2，
解得：x=5，
∴EC=5，
∴S菱形AECF=EC•AB=5×4=20．
点评：此题考查了菱形的性质、矩形的性质以及勾股定理．此题难度适中，注意掌握数形结合思想与方程思想的应用．
练习册系列答案
相关题目
把函数y=x2-4x+6的图象向左平移1个单位，再向上平移1个单位，所得图象对应的函数的解析式是（ ）
| A、y=（x-3）2+3 |
| B、y=（x-3）2+1 |
| C、y=（x-1）2+3 |
| D、y=（x-1）2+1 |
四边形ABCD在平面直角坐标系中的位置，如图所示，已知A（-2，-3），B（2，-2），C（3，1），D（-1，0），求证：四边形ABCD是平行四边形．
如图，正方形A，B，C，D的顶点ABCD都在坐标轴上，已知OA=OB=OC=OD=
如图，已知?ABCD中，过对角线的交点O的直线交CB，AD的延长线于E和F，证明：BE=DF．
如图，菱形ABCD中，O为AC上一点，OA=AB，经过B、C、D三点的⊙O的半径为1，求cos∠AOB的值．
如图，公园内有一边长为20米的正方形空地，先要在阴影部分种上绿化，求阴影部分的面积．（结果保留三个有效数字）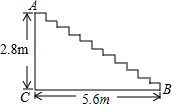
如图，某商场重新装修后，准备在大厅的主楼梯上铺设一种红色的地毯，已知这种地毯的价格为40元/m2，主楼梯的宽为3m，其侧面如图所示，则铺设这段楼梯至少需要多少元？
如图，如果AC⊥BC，CD⊥AB，∠1=∠2，那么下列结论中正确的个数是（ ）