题目内容
19. 如图,直线AC∥BD,P在直线AB上(不与点A,B重合).
如图,直线AC∥BD,P在直线AB上(不与点A,B重合).(1)当点P在如图所示的位置时,∠PCA=30°,∠PDB=25°,则∠CPD=55°.
(2)猜想,当点P在A,B两点之间运动时,∠PCA,∠PDB,∠CPD之间的数量关系∠CPD=∠PCA+∠PDB.
(3)说明(2)中的猜想成立的理由.
(4)当点P在直线AB上(不在线段AB上)运动时,试探究∠PCA,∠PDB,∠CPD之间的数量关系(画图并直接写出结论即可)
分析 (1)如图①,过P点作PE∥AC交CD于E点,由于AC∥BD,则PE∥BD,根据平行线的性质得∠CPE=∠PCA=20°,∠DPE=∠PDB=30°,所以∠CPD=50°;
(2)根据(1)可得结论;
(3)证明方法与(1)一样;
(4)过P点作PF∥BD交CD于F点,由于AC∥BD,则PF∥AC,根据平行线的性质得∠CPF=∠PCA,∠DPF=∠PDB,所以∠CPD=∠PCA-∠PDB.
解答 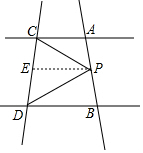 解:(1)如图①,过P点作PE∥AC交CD于E点,
解:(1)如图①,过P点作PE∥AC交CD于E点,
∵AC∥BD
∴PE∥BD,
∴∠CPE=∠PCA=30°,∠DPE=∠PDB=25°,
∴∠CPD=∠CPE+∠DPE=55°,
故答案为:55;
(2)∠CPD=∠PCA+∠PDB,
故答案为:∠CPD=∠PCA+∠PDB;
(3)过P点作PE∥AC交CD于E点,
∵AC∥BD
∴PE∥BD,
∴∠CPE=∠PCA,∠DPE=∠PDB,
∴∠CPD=∠CPE+∠DPE;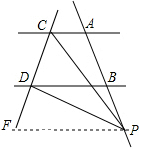
(3)∠CPD=∠PCA-∠PDB.理由如下:
如图②,过P点作PF∥BD交CD于F点,
∵AC∥BD,
∴PF∥AC,
∴∠CPF=∠PCA,∠DPF=∠PDB,
∴∠CPD=∠CPF-∠DPF=∠PCA-∠PDB.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.合理添加平行线是解决此题的关键.

练习册系列答案
相关题目
4.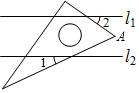 已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )
已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )
 已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )
已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
11.下列分解因式正确的是( )
| A. | 9m2-4n2=(9m+4n)(9m-4n) | B. | a2-4=(a-2)2 | ||
| C. | 9-6a+a2=(a-3)2 | D. | x2-3x+1=x(x-3)+1 |
 如图,△ABC是等边三角形,延长BA到点D,延长CB到点E,使BE=AD,连接CD,AE.
如图,△ABC是等边三角形,延长BA到点D,延长CB到点E,使BE=AD,连接CD,AE.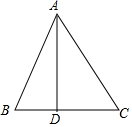 如图,在△ABC中,AB=26,BC=28,AC=30,求BC边上的高AD.
如图,在△ABC中,AB=26,BC=28,AC=30,求BC边上的高AD.