题目内容
13.观察下列等式:32-12=8×1;52-32=8×2;72-52=8×3;…,请用含正整数n的等式表示你所发现的规律:(2n+1)2-(2n-1)2=8n.分析 由等式可以看出:等式的左边是连续奇数的平方差,右边是8的倍数,由此规律得出答案即可.
解答 解:∵32-12=8=8×1;
52-32=16=8×2;
72-52=24=8×3;
…
∴第n个等式为(2n+1)2-(2n-1)2=8n.
故答案为:(2n+1)2-(2n-1)2=8n.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题.

练习册系列答案
相关题目
4.不等式组$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$的解集中任何x的值均在2≤x≤5的范围内,则a的取值范围是( )
| A. | a≥2 | B. | 2≤a≤4 | C. | a≤4 | D. | a≥2且a≠4 |
18. 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )| A. | 大于90° | B. | 等于90° | C. | 小于90° | D. | 无法确定 |
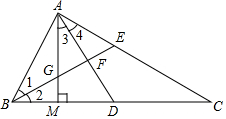 如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,AD平分∠MAC,交BC于点D,AM交BE于点G.
如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,AD平分∠MAC,交BC于点D,AM交BE于点G.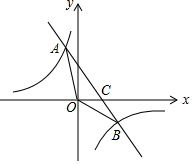 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A的坐标为(-3,n),线段OB=10,且sin∠BOC=$\frac{3}{5}$.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A的坐标为(-3,n),线段OB=10,且sin∠BOC=$\frac{3}{5}$. 如图,∠ABC=∠BCD
如图,∠ABC=∠BCD 如图,直线AC∥BD,P在直线AB上(不与点A,B重合).
如图,直线AC∥BD,P在直线AB上(不与点A,B重合).