题目内容
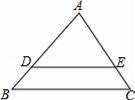
如图，在△ABC中，AB=AC，过A点作AD∥BC，若∠BAD=110°，则∠BAC的大小为（ ）
A．30° B．40° C．50° D．70°
B【考点】等腰三角形的性质；平行线的性质．
【分析】根据平行线的性质求出∠C，根据等腰三角形的性质得出∠B=∠C=70°，根据三角形内角和定理求出即可．
【解答】解：∵AB=AC，
∴∠B=∠C，
∵AD∥BC，∠1=70°，
∴∠C=∠1=70°，
∴∠B=70°，
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣70°=40°，
故选B．
【点评】本题考查了三角形内角和定理，等腰三角形的性质，平行线的性质的应用，解此题的关键是求出∠C的度数和得出∠B=∠C，注意：三角形内角和等于180°，两直线平行，内错角相等．
练习册系列答案
阅读快车系列答案
相关题目
（x＞0）的图象经过该菱形对角线的交点A，且与边BC交于点F．若点D的坐标为（6，8），则点A的坐标是 ．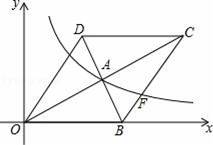
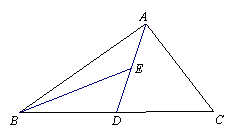（3） 若△ABC面积为20,过点C作CF//AD交BA的延长线于点F，求△BCF的面积。（友情提示：两条平行线间的距离处处相等.）
÷3
×
