题目内容
1.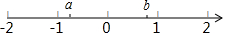 实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$-$\sqrt{(b-1)^{2}}$-$\sqrt{(a-b)^{2}}$.
实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$-$\sqrt{(b-1)^{2}}$-$\sqrt{(a-b)^{2}}$.
分析 根据数轴上点的位置判断出a+1,b-1,a-b的正负,原式利用二次根式性质及绝对值的代数意义化简,计算即可得到结果.
解答 解:根据题意得:-1<a<0<b<1,
∴a+1>0,b-1<0,a-b<0,
则原式=|a+1|-|b-1|-|a-b|=a+1+b-1+a-b=2a.
点评 此题考查了二次根式的性质与化简,以及实数与数轴,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.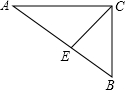 如图,在△ABC中,CE是角平分线,∠ACB=90°,若∠A=35°,则∠CEB的度数为( )
如图,在△ABC中,CE是角平分线,∠ACB=90°,若∠A=35°,则∠CEB的度数为( )
 如图,在△ABC中,CE是角平分线,∠ACB=90°,若∠A=35°,则∠CEB的度数为( )
如图,在△ABC中,CE是角平分线,∠ACB=90°,若∠A=35°,则∠CEB的度数为( )| A. | 70° | B. | 75° | C. | 80° | D. | 90° |
16.一元二次方程x2-2x-3=0 的两根分别是x1、x2,则x1+x2的值是( )
| A. | 3 | B. | 2 | C. | -3 | D. | -2 |
13.下列计算,正确的是( )
| A. | x4-x3=x | B. | x6÷x3=x2 | C. | x•x3=x4 | D. | (ax3)2=ax6 |
11.已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如表所示:
(1)顶点坐标为(2,0);
(2)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式:y=(x-5)2;
(3)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)都在二次函数y=ax2+bx+c的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?
| x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | 9 | … |
(2)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式:y=(x-5)2;
(3)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)都在二次函数y=ax2+bx+c的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?
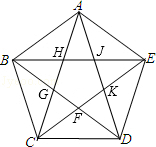 如图,向正五边形ABCDE区域内均匀掷点,落在五边形FGHJK区域内的概率为$\frac{7-3\sqrt{5}}{2}$.
如图,向正五边形ABCDE区域内均匀掷点,落在五边形FGHJK区域内的概率为$\frac{7-3\sqrt{5}}{2}$.