题目内容
19. 如图,水平放置的圆柱形排水管道的截面直径是1m,排水管内水的最大深度CD是0.8m,则水面宽AB为0.8m.
如图,水平放置的圆柱形排水管道的截面直径是1m,排水管内水的最大深度CD是0.8m,则水面宽AB为0.8m.
分析 连接OB,根据OB=OD可得出OC的长,再由勾股定理求出BC的长,进而可得出结论.
解答  解:连接OB,
解:连接OB,
∵排水管道的截面直径是1m,CD=0.8m,
∴OB=OD=0.5m,
∴OC=0.8-0.5=0.3m,
∴BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=$\sqrt{0.{5}^{2}-0.{3}^{2}}$=0.4m,
∴AB=2BC=0.8m.
故答案为:0.8.
点评 本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
14.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…解答下列问题:3+32+33+34+…+32014的末位数字是( )
| A. | 2 | B. | 3 | C. | 7 | D. | 9 |
11.已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如表所示:
(1)顶点坐标为(2,0);
(2)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式:y=(x-5)2;
(3)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)都在二次函数y=ax2+bx+c的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?
| x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | 9 | … |
(2)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式:y=(x-5)2;
(3)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)都在二次函数y=ax2+bx+c的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?
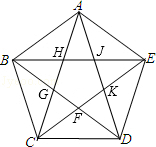 如图,向正五边形ABCDE区域内均匀掷点,落在五边形FGHJK区域内的概率为$\frac{7-3\sqrt{5}}{2}$.
如图,向正五边形ABCDE区域内均匀掷点,落在五边形FGHJK区域内的概率为$\frac{7-3\sqrt{5}}{2}$.