题目内容
 如图,已知抛物线与x轴分别交与点A、B,与y轴交与点C,根据图象中的信息解决下列问题:
如图,已知抛物线与x轴分别交与点A、B,与y轴交与点C,根据图象中的信息解决下列问题:(1)求这个二次函数的解析式;
(2)若y随x的增大而增大,则x的取值范围是
(3)已知一次函数y=kx+b经过A、C两点,若点P(x1,y1)在一次函数图象上,点Q(x2,y2)在二次函数图象上,当y1>y2时,请直接写出x的取值范围?
考点:二次函数与不等式(组),二次函数的性质,待定系数法求二次函数解析式
专题:
分析:(1)设二次函数的解析式为y=ax2+bx+c(a≠0),然后利用待定系数法求二次函数解析式解答;
(2)求出对称轴解析式,再根据二次函数的增减性解答;
(3)写出一次函数图象在二次函数图象上方部分的x的取值范围即可.
(2)求出对称轴解析式,再根据二次函数的增减性解答;
(3)写出一次函数图象在二次函数图象上方部分的x的取值范围即可.
解答:解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0),
由题意得,
,
解得
,
所以,y=-x2+4x+5;
(2)对称轴为直线x=-
=2,
所以,y随x的增大而增大,x的取值范围是x<2;
故答案为:.
(3)由图可知,y1>y2时,x的取值范围是x<0或x>5.
由题意得,
|
解得
|
所以,y=-x2+4x+5;
(2)对称轴为直线x=-
| 4 |
| 2×(-1) |
所以,y随x的增大而增大,x的取值范围是x<2;
故答案为:.
(3)由图可知,y1>y2时,x的取值范围是x<0或x>5.
点评:本题考查了二次函数与一次函数,待定系数法求二次函数解析式,二次函数的性质,此类题目,利用数形结合的思想求不等式的解集更简便.

练习册系列答案
相关题目
 张师傅不小心将一块三角形玻璃打破成如图中的三块,他准备去店里重新配置一块与原来一模一样的,最省事的做法是( )
张师傅不小心将一块三角形玻璃打破成如图中的三块,他准备去店里重新配置一块与原来一模一样的,最省事的做法是( )| A、带Ⅰ去 | B、带Ⅱ去 |
| C、带Ⅲ去 | D、三块全带去 |
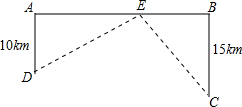 如图,河岸上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB与点B,已知DA=10km,CB=15km,现在AB上建一个水泵站E,使得C,D两村到E站的距离相等.求E应建在距A多远处?
如图,河岸上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB与点B,已知DA=10km,CB=15km,现在AB上建一个水泵站E,使得C,D两村到E站的距离相等.求E应建在距A多远处?