题目内容
解方程
(1)2(x-3)2=8;
(2)3x2-6x=-3;
(3)x(x-2)=x-2;
(4)(x+8)(x+1)=-12.
(1)2(x-3)2=8;
(2)3x2-6x=-3;
(3)x(x-2)=x-2;
(4)(x+8)(x+1)=-12.
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-配方法
专题:
分析:(1)用直接开平方法解答;
(2)利用完全平方公式后直接开平方;
(3)移项后提公因式;
(4)化为一般形式后用十字相乘法解答.
(2)利用完全平方公式后直接开平方;
(3)移项后提公因式;
(4)化为一般形式后用十字相乘法解答.
解答:解:(1)2(x-3)2=8;
两边同时除以2得(x-3)2=4,
开方得x-3=±2,
解得x1=5,x2=1.
(2)3x2-6x=-3;
移项得3x2-6x+3=0,
两边同时除以3得,x2-2x+1=0,
即(x-1)2=0,
开方得x-1=0,
x1=x2=1;
(3)x(x-2)=x-2;
移项得x(x-2)-(x-2)=0,
提公因式得(x-2)(x-1)=0,
解得x1=2,x2=1;
(4)(x+8)(x+1)=-12,
原式可化为x2+9x+20=0,
因式分解得(x+4)(x+5)=0,
解得x1=-4,x2=-5.
两边同时除以2得(x-3)2=4,
开方得x-3=±2,
解得x1=5,x2=1.
(2)3x2-6x=-3;
移项得3x2-6x+3=0,
两边同时除以3得,x2-2x+1=0,
即(x-1)2=0,
开方得x-1=0,
x1=x2=1;
(3)x(x-2)=x-2;
移项得x(x-2)-(x-2)=0,
提公因式得(x-2)(x-1)=0,
解得x1=2,x2=1;
(4)(x+8)(x+1)=-12,
原式可化为x2+9x+20=0,
因式分解得(x+4)(x+5)=0,
解得x1=-4,x2=-5.
点评:本题考查了一元二次方程的解法,要根据不同方程,选择合适的方法.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
 如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.△ABC的面积为70,AB=16,BC=12.求DE的长.
如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.△ABC的面积为70,AB=16,BC=12.求DE的长.
 如图,已知抛物线与x轴分别交与点A、B,与y轴交与点C,根据图象中的信息解决下列问题:
如图,已知抛物线与x轴分别交与点A、B,与y轴交与点C,根据图象中的信息解决下列问题: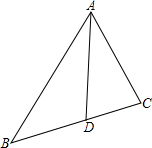 如图,△ABC的角平分线AD交BC于点D,
如图,△ABC的角平分线AD交BC于点D,