Question

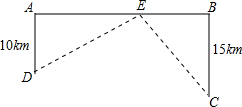如图，河岸上A、B两点相距25km，C、D为两村庄，DA⊥AB于点A，CB⊥AB与点B，已知DA=10km，CB=15km，现在AB上建一个水泵站E，使得C，D两村到E站的距离相等．求E应建在距A多远处？

Answer 1

考点：全等三角形的应用

专题：

分析：关键描述语：产品收购站E，使得C、D两村到E站的距离相等，在Rt△DAE和Rt△CBE中，设出AE的长，可将DE和CE的长表示出来，列出等式进行求解即可．

解答：解：设AE=xkm，
∵C、D两村到E站的距离相等，
∴DE=CE，即DE²=CE²，
由勾股定理，得10²+x²=15²+（25-x）²，
解得：x=15．
故：E点应建在距A站15千米处．

点评：本题主要考查了勾股定理的应用，运用勾股定理将两个直角三角形的斜边表示出来，两边相等求解是解题关键．