题目内容
10. 如图,在平面直角坐标系中,A(0,3),B(4,0),P为线段OB(不包括端点)上的一个动点,将△AOP沿AP对折,O的对称点记为E.
如图,在平面直角坐标系中,A(0,3),B(4,0),P为线段OB(不包括端点)上的一个动点,将△AOP沿AP对折,O的对称点记为E.(1)求PE+PB的长;
(2)求△BEP周长的最小值;
(3)过A作AP的垂线交PE的延长线于点Q,在点P的运动过程中,点Q到x轴的距离是否发生变化?如果不变,请求出该距离;如果变化,请说明理由.
分析 (1)由折叠得到OP=PE,即可得到PE+PB=OB=4;
(2)先由勾股定理求出AB,求出BE,即可;
(3)先判断出△DAP≌△QAP,得到$\frac{AD}{DQ}$=$\frac{1}{2}$,在判断出△DAO∽△DQF,即可.
解答 (1)由折叠得OP=PE,
∴PE+PB=OP+PB=OB=4;
(2)由折叠得,AE=AO=3,EP=OP
∵△BEP周长=EP+PB+EB=OP+PB+EB=OB+EB=4+EB
要使△BEP周长最小,只要EB最小即可,
∴EB⊥PQ时,EB最小,
而AE⊥PQ,
∴点E在AB上时,EB最小.
在Rt△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,EB=AB-AE=2,
∴△PEB的周长=EP+PB+EB=OB+BE=6.
(3)点Q到x轴距离不变
如图,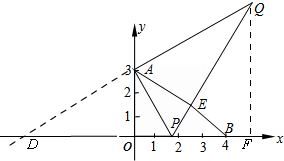
延长QA交x轴于点D,作QF⊥x轴于F
∵AQ⊥AP,
∴∠QAP=∠DAP=90°
∵∠DPA=∠EPA,AP=AP
∴△DAP≌△QAP,
∴AD=AQ
∴$\frac{AD}{DQ}$=$\frac{1}{2}$
∵AO⊥x轴,QF⊥x轴
∴AO∥QF
∴△DAO∽△DQF
∴$\frac{AO}{QF}=\frac{DA}{DQ}$=$\frac{1}{2}$
∴QF=2AO=6
∴点Q到x轴的距离为6,
点评 此题是几何变换综合题,主要考查了勾股定理的运用,相似三角形的性质和判定,全等三角形的性质和判定,解本题的关键是判定△DAP≌△QAP.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
20.某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,
以下说法正确的是( )
| 劳动时间(小时) | 3 | 4 | 5 | 6 |
| 人数 | 1 | 1 | 2 | 1 |
| A. | 中位数是5,平均数是3.6 | B. | 众数是5,平均数是4.6 | ||
| C. | 中位数是4,平均数是3.6 | D. | 众数是2,平均数是4.6 |

 如图,一次函数y=$\frac{1}{2}$x+2的图象在x、y轴上的交点为A、B,点P是该一次函数的图象上位于x轴上方的一点,作PQ⊥x轴于点Q,以PQ的右侧作正方形PQMN.
如图,一次函数y=$\frac{1}{2}$x+2的图象在x、y轴上的交点为A、B,点P是该一次函数的图象上位于x轴上方的一点,作PQ⊥x轴于点Q,以PQ的右侧作正方形PQMN.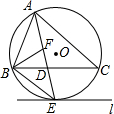 如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.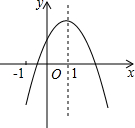 二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P,Q的大小关系是P>Q.
二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P,Q的大小关系是P>Q. 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为$\sqrt{7}$.
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为$\sqrt{7}$.