题目内容
5.如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,AB的垂直平分线交AB于点E,交射线BC于点F,点P从点A出发沿射线AC以每秒2$\sqrt{3}$个单位的速度运动,同时点Q从点C出发沿CB方向以每秒1个单位的速度运动,当点Q到达点B时,点P,Q同时停止运动.设运动的时间为t秒.(1)当t为何值时,PQ∥EF;
(2)当点P在C的左侧时,记四边形PFEQ的面积为s,请求出s关于t的函数关系式;s是否存在最大值?如有,请求出;如没有,请说明理由.
(3)设P,Q关于点C的对称点分别为P′,Q′,当t取何值时,线段P′Q′与线段EF相交?
分析 (1)根据相似三角形的性质得到$\frac{QC}{PC}=\frac{AC}{BC}$,代入数据解得t=$\frac{3}{5}$;
(2)作EH⊥AC于H,根据三角形的面积公式得到S=$\sqrt{3}$t2+$\frac{3\sqrt{3}}{4}$t-$\frac{\sqrt{3}}{4}$($\frac{1}{2}$<t≤1),当t≥-$\frac{3}{8}$时,s随t的增大而增大,于是得到当t=1时,S最大=$\frac{3\sqrt{3}}{2}$;
(3)如图3,设AC与EF交于点M,易得CM=$\frac{\sqrt{3}}{3}$,当CP′=CP≥CM,且CQ′=CQ≤CF时,线段P′Q′与线段EF相交,解不等式组即可得到结论
解答 解:(1)如图1,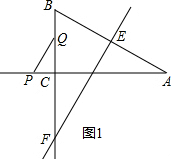
∵PQ∥EF,
∴△QPC∽△ABC,
∴$\frac{QC}{PC}=\frac{AC}{BC}$,
∴$\frac{t}{2\sqrt{3}t-\sqrt{3}}=\frac{\sqrt{3}}{1}$,解得:t=$\frac{3}{5}$;
∴当t为$\frac{3}{5}$时,PQ∥EF;
(2)如图2,作EH⊥AC于H,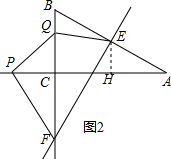
∴EH∥BC,
∵AE=BE,
∴AH=CH=$\frac{1}{2}$AC=1,
∵BF=2BE=2,
∴CF=1,
∴PH=2$\sqrt{3}$t-$\frac{1}{2}\sqrt{3}$,QF=t+1,
∴S=S△PQF+S△QEF=$\frac{1}{2}$QF•PC+$\frac{1}{2}$QF•CH=$\frac{1}{2}$•QF•PH=$\frac{1}{2}$(2$\sqrt{3}$t-$\frac{1}{2}$$\sqrt{3}$)(t+1)=$\sqrt{3}$t2+$\frac{3\sqrt{3}}{4}$t-$\frac{\sqrt{3}}{4}$($\frac{1}{2}$<t≤1),
当t≥-$\frac{3}{8}$时,s随t的增大而增大,
∵$\frac{1}{2}$<t≤1,
∴当t=1时,S最大=$\frac{3\sqrt{3}}{2}$;
(3)如图3,设AC与EF交于点M,易得CM=$\frac{\sqrt{3}}{3}$,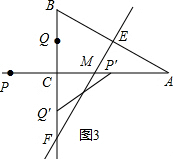
当CP′=CP≥CM,且CQ′=CQ≤CF时,
线段P′Q′与线段EF相交,
也就是$\left\{\begin{array}{l}{2\sqrt{3}t-\sqrt{3}≥\frac{\sqrt{3}}{3}}\\{t≤1}\end{array}\right.$,
解得$\frac{2}{3}$≤t≤1.
点评 本题考查了相似三角形的判定和性质,二次函数的性质,求二次函数的最值,特殊角的三角函数,解直角三角形,正确作出图形是解题的关键.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案| A. | $\left\{{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{8x+3=y}\\{7x-4=y}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{y-8x=3}\\{y-7x=4}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{8x-y=3}\\{7x-y=4}\end{array}}\right.$ |
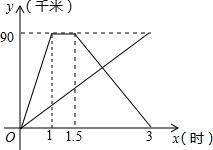 甲、乙两个人同时从相距90千米的A地前往B点,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们 离A地的距离y(千米)与时间x(时)之间的函数关系图象.
甲、乙两个人同时从相距90千米的A地前往B点,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们 离A地的距离y(千米)与时间x(时)之间的函数关系图象.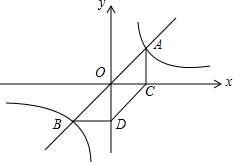 如图,一过原点的直线y=mx(m>0)与反比例函数$y=\frac{k}{x}$(k>0)的图象交于A、B两点,过A、B两点分别向x轴、y轴作垂线,垂足分别为C、D两点,连接CD.
如图,一过原点的直线y=mx(m>0)与反比例函数$y=\frac{k}{x}$(k>0)的图象交于A、B两点,过A、B两点分别向x轴、y轴作垂线,垂足分别为C、D两点,连接CD. 如图,在平面直角坐标系中,A(0,3),B(4,0),P为线段OB(不包括端点)上的一个动点,将△AOP沿AP对折,O的对称点记为E.
如图,在平面直角坐标系中,A(0,3),B(4,0),P为线段OB(不包括端点)上的一个动点,将△AOP沿AP对折,O的对称点记为E. 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论: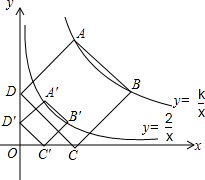 如图,正方形ABCD的顶点A,B在函数y=$\frac{k}{x}$(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
如图,正方形ABCD的顶点A,B在函数y=$\frac{k}{x}$(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变. 如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )
如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )


