题目内容
20. 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为$\sqrt{7}$.
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为$\sqrt{7}$.
分析 先利用等腰三角形的性质得到OC⊥AB,则利用勾股定理可计算出OC=$\sqrt{7}$,然后利用画法可得到OM=OC=$\sqrt{7}$,于是可确定点M对应的数.
解答 解:∵△ABC为等腰三角形,OA=OB=3,
∴OC⊥AB,
在Rt△OBC中,OC=$\sqrt{B{C}^{2}-O{B}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∵以O为圆心,CO长为半径画弧交数轴于点M,
∴OM=OC=$\sqrt{7}$,
∴点M对应的数为$\sqrt{7}$.
故答案为$\sqrt{7}$.
点评 本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.也考查了等腰三角形的性质.

练习册系列答案
相关题目
5.计算3a2-a2的结果是( )
| A. | 4a2 | B. | 3a2 | C. | 2a2 | D. | 3 |
12. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 2π | B. | π | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
9.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | (-2a2b)3=-6a6b3 | C. | $\sqrt{8}+\sqrt{2}=3\sqrt{2}$ | D. | (a+b)2=a2+b2 |
 如图,在平面直角坐标系中,A(0,3),B(4,0),P为线段OB(不包括端点)上的一个动点,将△AOP沿AP对折,O的对称点记为E.
如图,在平面直角坐标系中,A(0,3),B(4,0),P为线段OB(不包括端点)上的一个动点,将△AOP沿AP对折,O的对称点记为E.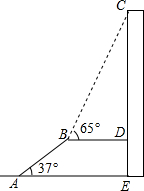 如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).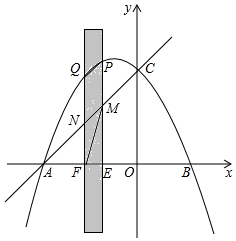 如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.
如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F. 如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )
如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )


