Question

7．如图，在平面直角坐标系中，点A的坐标是（1，2），连接OA，将线段OA绕着点O顺时针旋转，使点A的对应点A′恰好落在x轴正半轴上，则点A′的坐标是（$\sqrt{5}$，0）．

Answer 1

分析 先根据两点间的距离公式计算出OA=$\sqrt{5}$，再根据旋转的性质得到OA′=OA=$\sqrt{5}$，然后利用x轴上点的坐标特征写出点A′的坐标．

解答 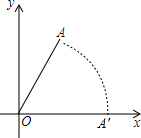解：如图，∵点A的坐标是（1，2），
∴OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
∵线段OA绕着点O顺时针旋转，使点A的对应点A′恰好落在x轴正半轴上，
∴OA′=OA=$\sqrt{5}$，
∴点A′的坐标是（$\sqrt{5}$，0）．
故答案为（$\sqrt{5}$，0）．

点评 本题考查了坐标与图形变化-旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．解决本题的关键是计算出OA的长．