题目内容
20.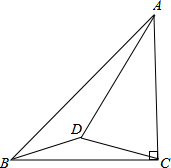 如图,△ABC中,AC=BC,∠ACB=90°,D是△ABC内一点,AD=AC,∠CAD=30°,试判断BD,CD的大小关系,并说明理由.
如图,△ABC中,AC=BC,∠ACB=90°,D是△ABC内一点,AD=AC,∠CAD=30°,试判断BD,CD的大小关系,并说明理由.
分析 作BE⊥BC,AE⊥AC,两线相交于点E,则四边形AEBC是正方形,由∠DAC=30°,得∠DAE=60°,由AD=AC,得AD=AE,所以,三角形AED是等边三角形,可得∠AED=60°,∠DEB=30°,所以,△ADC≌△EDB,可得BD=CD.
解答 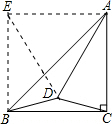 解:BD=CD.理由如下:
解:BD=CD.理由如下:
作BE⊥BC,AE⊥AC,两线相交于点E,
∵△ABC是等腰直角三角形,即AC=BC,
∴四边形AEBC是正方形,
∵∠DAC=30°,
∴∠DAE=60°,
∵AD=AC,
∴AD=AE,
∴△AED是等边三角形,
∴∠AED=60°,
∴∠DEB=30°,
在△ADC和△EDB中,
$\left\{\begin{array}{l}{AD=ED}\\{∠DAC=∠DEB=30°}\\{AC=EB}\end{array}\right.$,
∴△ADC≌△EDB(SAS),
∴CD=BD,即BD=CD.
点评 本题主要考查了等腰直角三角形的性质、等边三角形的性质和全等三角形的判定与性质,作辅助线构建正方形,通过证明三角形全等得出线段相等,是解答本题的基本思路.

练习册系列答案
相关题目
10.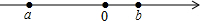 实数a、b在数轴上的位置如图所示,则a与b的大小关系是( )
实数a、b在数轴上的位置如图所示,则a与b的大小关系是( )
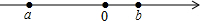 实数a、b在数轴上的位置如图所示,则a与b的大小关系是( )
实数a、b在数轴上的位置如图所示,则a与b的大小关系是( )| A. | a>b | B. | a<b | C. | a=b | D. | 不能判断 |
15.已知一个布袋里装有5个红球,3个白球,这些球除颜色外其余都相同.从该布袋里任意摸出1个球,若第一次是1个白球不放回,则第二次摸出白球的概率( )
| A. | $\frac{3}{8}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{28}$ | D. | $\frac{9}{64}$ |
12.小星同学参加体育测试的五次立定跳远的成绩(单位:米)是:1.2,1.3,1.2,1.0,1.1.这组数据的众数是( )
| A. | 1.0 | B. | 1.1 | C. | 1.2 | D. | 1.3 |
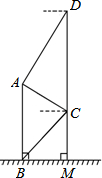 在数学活动课上,为测量教学楼前的一座雕塑AB的高度.小明在二楼C处,利用测角仪测得雕塑顶端A处的仰角为30°,底部B处的俯角为45°,小华在五楼D处,利用测角仪测得雕塑顶端A处的俯角为60°.若CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
在数学活动课上,为测量教学楼前的一座雕塑AB的高度.小明在二楼C处,利用测角仪测得雕塑顶端A处的仰角为30°,底部B处的俯角为45°,小华在五楼D处,利用测角仪测得雕塑顶端A处的俯角为60°.若CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).