题目内容
8.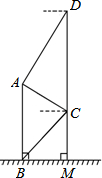 在数学活动课上,为测量教学楼前的一座雕塑AB的高度.小明在二楼C处,利用测角仪测得雕塑顶端A处的仰角为30°,底部B处的俯角为45°,小华在五楼D处,利用测角仪测得雕塑顶端A处的俯角为60°.若CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
在数学活动课上,为测量教学楼前的一座雕塑AB的高度.小明在二楼C处,利用测角仪测得雕塑顶端A处的仰角为30°,底部B处的俯角为45°,小华在五楼D处,利用测角仪测得雕塑顶端A处的俯角为60°.若CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
分析 利用锐角三角函数关系得出AE、EC的长,进而利用等腰三角形的性质得出BE的长,即可得出答案.
解答 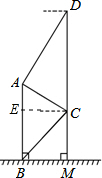 解:过点C作CE⊥AB于E.
解:过点C作CE⊥AB于E.
∵∠D=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=10,
∴AC=$\frac{1}{2}$CD=5.
在RT△ACE中,
AE=AC•sin∠ACE=5×sin30°=$\frac{5}{2}$,CE=AC•cos∠ACE=5×cos30°=$\frac{5}{2}$$\sqrt{3}$,
在RT△BDE中,
∵∠BCE=45°,
∴BE=CE•tan45°=$\frac{5}{2}$$\sqrt{3}$,
∴AB=AE+BE=$\frac{5}{2}$+$\frac{5}{2}$$\sqrt{3}$=$\frac{5}{2}$($\sqrt{3}$+1)≈6.8(米).
答:雕塑AB的高度约为6.8米.
点评 此题主要考查了解直角三角形的应用,得出AE、BE的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
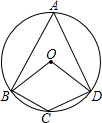 如图,四边形ABCD是⊙O的内接四边形,若∠C=130°,则∠BOD=100°.
如图,四边形ABCD是⊙O的内接四边形,若∠C=130°,则∠BOD=100°.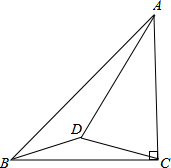 如图,△ABC中,AC=BC,∠ACB=90°,D是△ABC内一点,AD=AC,∠CAD=30°,试判断BD,CD的大小关系,并说明理由.
如图,△ABC中,AC=BC,∠ACB=90°,D是△ABC内一点,AD=AC,∠CAD=30°,试判断BD,CD的大小关系,并说明理由.