题目内容
9.(1)计算:$\sqrt{12}$+(-$\frac{1}{3}$)0-|$\sqrt{3}$-1|-2sin60°(2)解不等式组:$\left\{\begin{array}{l}2-3(x-3)≤5\\ \frac{1+2x}{3}>x-1\end{array}$并把解集在数轴上表示出来.
分析 (1)首先根据算术平方根、零指数幂的运算方法,以及60°的三角函数值,还有绝对值的求法计算,然后根据加法交换律和加法结合律,求出算式$\sqrt{12}$+(-$\frac{1}{3}$)0-|$\sqrt{3}$-1|-2sin60°的值是多少即可.
(2)首先根据解一元一次不等式组的方法,分别求出不等式组中每个不等式的解集,再求出不等式组的解集是多少;然后把不等式的解集在数轴上表示出来即可.
解答 解:(1)$\sqrt{12}$+(-$\frac{1}{3}$)0-|$\sqrt{3}$-1|-2sin60°
=2$\sqrt{3}+1-(\sqrt{3}-1)-2×\frac{\sqrt{3}}{2}$
=2$\sqrt{3}+1-\sqrt{3}+1-\sqrt{3}$
=(2$\sqrt{3}-\sqrt{3}-\sqrt{3}$)+(1+1)
=0+2
=2
(2)由2-3(x-3)≤5,可得x≥2,
由$\frac{1+2x}{3}>x-1$,可得x<4,
所以不等式组:$\left\{\begin{array}{l}2-3(x-3)≤5\\ \frac{1+2x}{3}>x-1\end{array}$的解集是:2≤x<4,
在数轴上表示为: .
.
点评 (1)此题主要考查了算术平方根的含义以及求法,以及绝对值的含义和求法,要熟练掌握.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:(1)a0=1(a≠0);(2)00≠1.
(3)此题还考查了特殊角的三角函数值,要牢记30°、45°、60°等特殊角的三角函数值.
(4)此题还考查了一元一次不等式组的解法,要熟练掌握,解答此题的关键是要明确解一元一次不等式组的步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.

| 月用水量/m3 | 8 | 9 | 10 | 11 | 12 |
| 户 数/个 | 3 | 4 | 6 | 4 | 3 |
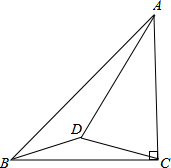 如图,△ABC中,AC=BC,∠ACB=90°,D是△ABC内一点,AD=AC,∠CAD=30°,试判断BD,CD的大小关系,并说明理由.
如图,△ABC中,AC=BC,∠ACB=90°,D是△ABC内一点,AD=AC,∠CAD=30°,试判断BD,CD的大小关系,并说明理由. 如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成50°角,在离电线杆底部D点6米的B处安置测角仪,测角仪高AB为1.5米,在A处测得电线杆上C处的仰角为32°,求拉线CE的长(结果精确到0.1米).(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.63,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成50°角,在离电线杆底部D点6米的B处安置测角仪,测角仪高AB为1.5米,在A处测得电线杆上C处的仰角为32°,求拉线CE的长(结果精确到0.1米).(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.63,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).