题目内容
已知函数y=(2m-2)x+(m+1)
(1)m为何值时,图象过原点.
(2)已知y随x增大而增大,求m的取值范围.
(3)函数图象与y轴交点在x轴上方,求m取值范围.
(1)m为何值时,图象过原点.
(2)已知y随x增大而增大,求m的取值范围.
(3)函数图象与y轴交点在x轴上方,求m取值范围.
考点:一次函数图象与系数的关系
专题:计算题
分析:(1)利用图象与y轴的交点坐标为(0,m+1)得到m+1=0,然后解方程;
(2)根据已次函数的性质得2m-2>0,然后解不等式;
(3)利用图象与y轴的交点坐标为(0,m+1)可得m+1>0,然后解不等式.
(2)根据已次函数的性质得2m-2>0,然后解不等式;
(3)利用图象与y轴的交点坐标为(0,m+1)可得m+1>0,然后解不等式.
解答:解:(1)根据题意得m+1=0,
解得m=-1,
即m为1时,图象过原点;
(2)当2m-2>0时,y随x增大而增大,
所以m>1;
(3)m+1>0,即得m>-1,
即当m>-1时,函数图象与y轴交点在x轴上方.
解得m=-1,
即m为1时,图象过原点;
(2)当2m-2>0时,y随x增大而增大,
所以m>1;
(3)m+1>0,即得m>-1,
即当m>-1时,函数图象与y轴交点在x轴上方.
点评:本题考查了一次函数图象与系数的关系:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
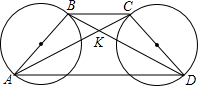 如图,梯形ABCD两对角线交于点K,分别以AB、CD为直径各作一圆,K位于两圆之外.证明:由点K向这两个圆所作的切线长相等.
如图,梯形ABCD两对角线交于点K,分别以AB、CD为直径各作一圆,K位于两圆之外.证明:由点K向这两个圆所作的切线长相等.