题目内容
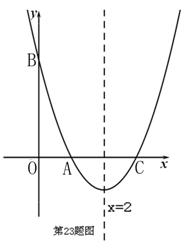
如图,四 边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在
边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在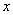 轴上,直线BD交
轴上,直线BD交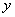 轴于点F,交OE于点H,线段BC、OC的长是方程
轴于点F,交OE于点H,线段BC、OC的长是方程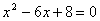 的两个根,且OC>BC.
的两个根,且OC>BC.
(1)求直线BD的解析式.
(2)求 △OFH的面积.
(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
 |
解:(1)x2-6x+8=0
x1=2,x2=4
∵OC > BC
∴OC=4,BC=2
B(-2,4)
∵OD=OC=4 ∴D(4,0) …………………………………………………………1分
设BD解析式为y=kx+b (k≠0)
 ∴ -2k+b=4 ∴ k=
∴ -2k+b=4 ∴ k=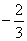 ………………………………2分
………………………………2分
4k+b=0 b=
b=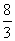
∴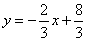 ………………………………………………1分
………………………………………………1分
(2) ∵DE=2, ∴E(4,2)∴直线OE:y=
 …………………………………………1分
…………………………………………1分
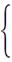 ∴
∴ 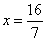
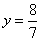
∴H(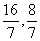 ) ………………………………………1分
) ………………………………………1分
当x=0,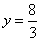 ∴S△OFH =
∴S△OFH =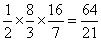 ………………………………………1分
………………………………………1分
(3) 存在N1(4,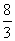 ),N2(
),N2(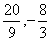 ), N3(-4,-
), N3(-4,-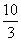 ) …………………………………3分
) …………………………………3分

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0)、(x2,0),且x1<x2,图象上有一点M(x0,y0),在x轴下方,则下列判断正确的是( )
|
| A. | a(x0﹣x1)(x0﹣x2)<0 | B. | a>0 |
|
| C. | b2﹣4ac≥0 | D. | x1<x0<x2 |
 如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间
如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间
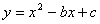 交
交