题目内容
若二次函数y=ax2+bx+c（a≠0）的图象与x轴有两个交点，坐标分别为（x1，0）、（x2，0），且x1＜x2，图象上有一点M（x0，y0），在x轴下方，则下列判断正确的是（ ）
|
| A． | a（x0﹣x1）（x0﹣x2）＜0 | B． | a＞0 |
|
| C． | b2﹣4ac≥0 | D． | x1＜x0＜x2 |
A解：A、当a＞0时，
∵点M（x0，y0），在x轴下方，
∴x1＜x0＜x2，
∴x0﹣x1＞0，x0﹣x2＜0，
∴a（x0﹣x1）（x0﹣x2）＜0；
当a＜0时，若点M在对称轴的左侧，则x0＜x1＜x2，
∴x0﹣x1＜0，x0﹣x2＜0，
∴a（x0﹣x1）（x0﹣x2）＜0；
若点M在对称轴的右侧，则x1＜x2＜x0，
∴x0﹣x1＞0，x0﹣x2＞0，
∴a（x0﹣x1）（x0﹣x2）＜0；
综上所述，a（x0﹣x1）（x0﹣x2）＜0，故本选项正确；
B、a的符号不能确定，故本选项错误；
C、∵函数图象与x轴有两个交点，∴△＞0，故本选项错误；
D、x1、x0、x2的大小无法确定，故本选项错误．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
π 
，则当函数值y=8时，自变量x的值是（ ）
B． 4 C． ±
上，点B在双曲线y=
上，且AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则它的面积为 
2015年某中学举行的春季田径径运动会上，参加男子跳高的15名运动员的成绩如表所示：
| 成绩（m） | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是（ ）
|
| A． | 1.70m，1.65m | B． | 1.70m，1.70m | C． | 1.65m，1.60m | D． | 3，4 |
取1.732，结果保留整数）
﹣
）×
= ．
边形OABC是矩形,点A、C在坐标轴上，△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在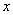
轴上，直线BD交
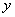轴于点F,交OE于点H,线段BC、OC的长是方程
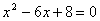的两个根，且OC＞BC.