题目内容
若n(n≠0)是关于x的一元二次方程x2+mx+2n=0的一个根,则n+m+4的值为 .
考点:一元二次方程的解
专题:计算题
分析:根据一元二次方程的解的定义把x=n代入x2+mx+2n=0得到x2+mx+2n=0得n+m=-2,然后利用整体代入的方法进行计算.
解答:解:∵n(n≠0)是关于x的一元二次方程x2+mx+2n=0的一个根,
∴n2+mn+2n=0,
∴n+m=-2,
∴n+m+4=-2+4=2.
故答案为2.
∴n2+mn+2n=0,
∴n+m=-2,
∴n+m+4=-2+4=2.
故答案为2.
点评:本题考查了一元二次方程的解(根):能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
相关题目
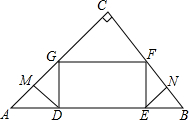 如图,在△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上,若∠ACB=90°,线段DM、EN分别为∠ADG和∠BEF的角平分线.求证:MG=NF.
如图,在△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上,若∠ACB=90°,线段DM、EN分别为∠ADG和∠BEF的角平分线.求证:MG=NF.