题目内容
3.请写一个二次函数,使它满足两个条件:(1)函数图象的开口向下;(2)函数图象经过点(-1,2),你的结果是y=-x2+3(本题答案不唯一).分析 根据题意可知a<0,可设抛物线的解析式为y=-x2+c,将(-1,2)代入即可求出a的值.
解答 解:设y=-x2+c
将(-1,2)代入y=-x2+c,
∴c=3,
∴y=-x2+3
故答案为:y=-x2+3(本题答案不唯一)
点评 本题考查二次函数的性质,解题的关键是根据题意可知a<0,然后用待定系数法求出解析式,本题属于基础题型.

练习册系列答案
相关题目
18.春节期间嘉嘉去距家10千米的电影院看电影,计划骑自行车和坐公交车两种方式,已知汽车的速度是骑车速度的2倍,若坐公交车可以从家晚15分钟出发恰好赶上公交车,结果与骑自行车同时到达,设骑车学生的速度为x千米/小时,则所列方程正确的是( )
| A. | $\frac{10}{x}$-$\frac{10}{2x}$=15 | B. | $\frac{10}{2x}$-$\frac{10}{x}$=15 | C. | $\frac{10}{x}$-$\frac{10}{2x}$=$\frac{1}{4}$ | D. | $\frac{10}{2x}$-$\frac{10}{x}$=$\frac{1}{4}$ |
18.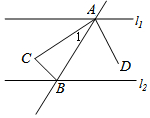 如图,已知l1∥l2,AC、BC、AD为三条角平分线,则图中与∠1互为余角的角有( )
如图,已知l1∥l2,AC、BC、AD为三条角平分线,则图中与∠1互为余角的角有( )
 如图,已知l1∥l2,AC、BC、AD为三条角平分线,则图中与∠1互为余角的角有( )
如图,已知l1∥l2,AC、BC、AD为三条角平分线,则图中与∠1互为余角的角有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
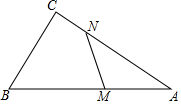 已知,在△ACB中,BC=9,AC=12,AB=15.若线段AB上有一点动点M,线段AC上有一动点N,始终保持AM=CN,若△AMN是直角三角形,且MN=4,则AM的长为$\frac{16}{3}$.
已知,在△ACB中,BC=9,AC=12,AB=15.若线段AB上有一点动点M,线段AC上有一动点N,始终保持AM=CN,若△AMN是直角三角形,且MN=4,则AM的长为$\frac{16}{3}$.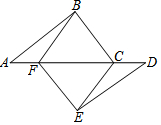 如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.
如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.