题目内容
18．
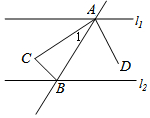如图，已知l1∥l2，AC、BC、AD为三条角平分线，则图中与∠1互为余角的角有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据平行线的性质，以及角平分线的定义，可得∠1与∠2互余，∠1与∠3互余，∠1与∠4互余，∠1与∠5互余．
解答 
解：∵l1∥l2，且AC、BC、AD为三条角平分线，
∴∠1+∠2=$\frac{1}{2}$×180°=90°，
∴∠1与∠2互余，
又∵∠2=∠3，
∴∠1与∠3互余，
∵∠CAD=∠1+∠4=$\frac{1}{2}$×180°=90°，
∴∠1与∠4互余，
又∵∠4=∠5，
∴∠1与∠5互余，
故与∠1互余的角共有4个．
故选：D．
点评 本题主要考查了平行线的性质，解题时注意：两直线平行，同旁内角互补．
练习册系列答案
相关题目
13．下列几何体中，正视图是矩形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
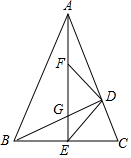已知：如图，在△ABC中，∠BAC=45°，BD、AE分别是边AC、BC边上的高，AE和BD交于点G，点E、点F分别是BC、AG的中点．判断△DEF的形状，并说明理由．
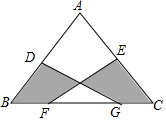如图，在△ABC中，AB=AC=10，BC=12，D、E分别为AB，AC中点，F、G为线段BC上两点，且FG=6，则阴影部分面积为24．
13．下列叙述正确的是（ ）
| A． | 平分弦的直径垂直于弦 | B． | 三角形的外心到三边的距离相等 | ||
| C． | 三角形的内心到三边的距离相等 | D． | 相等的圆周角所对的弧相等 |