题目内容
11.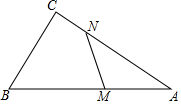 已知,在△ACB中,BC=9,AC=12,AB=15.若线段AB上有一点动点M,线段AC上有一动点N,始终保持AM=CN,若△AMN是直角三角形,且MN=4,则AM的长为$\frac{16}{3}$.
已知,在△ACB中,BC=9,AC=12,AB=15.若线段AB上有一点动点M,线段AC上有一动点N,始终保持AM=CN,若△AMN是直角三角形,且MN=4,则AM的长为$\frac{16}{3}$.
分析 可设AM的长为x,则AN=12-x,在Rt△AMN中,根据勾股定理可求AM的长.
解答 解:设AM的长为x,则AN=12-x,
在Rt△AMN中,x2+42=(12-x)2,
解得x=$\frac{16}{3}$.
故AM的长为$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 此题考查了勾股定理在实际生活中的应用,解题的关键是从实际问题中整理出直角三角形求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列命题是假命题的是( )
| A. | 三角形的内心到三角形三条边的距离相等 | |
| B. | 三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等 | |
| C. | 对于实数a,b,若|a|≤|b|,则a≤b | |
| D. | 对于实数x,若$\sqrt{{x}^{2}}$=x,则x≥0 |
2.已知二次函数y=ax2+bx+c自变量x与函数值y之间满足下列数量关系,那么(a+b+c)($\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$)的值是24.
| x | 3 | 5 | 7 |
| y | 0.08 | 0.08 | 3 |
19.某超市在春节期间对顾客实行优惠,规定如下:
(1)刘老师一次性购物600元,求他实际付款多少元?
(2)若顾客在该超市一次性购物x元(x≥500),实际付款y元,请求出用含x的代数式表示y的式子.
(3)如果刘老师两次购物贷款合计820元,第一次购物的贷款为a元(200<a<300),用含a的代数式表示:两次购物刘老师实际多少元?
| 一次性购物 | 优惠方法 |
| 少于200元 | 不予优惠 |
| 低于500元但不低于200元 | 九折优惠 |
| 500元或超过500元 | 其中500元部分给予九折优惠,超过500元部分给予八折优惠 |
(2)若顾客在该超市一次性购物x元(x≥500),实际付款y元,请求出用含x的代数式表示y的式子.
(3)如果刘老师两次购物贷款合计820元,第一次购物的贷款为a元(200<a<300),用含a的代数式表示:两次购物刘老师实际多少元?
16.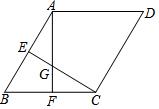 如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
 如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
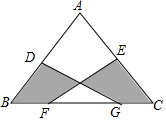 如图,在△ABC中,AB=AC=10,BC=12,D、E分别为AB,AC中点,F、G为线段BC上两点,且FG=6,则阴影部分面积为24.
如图,在△ABC中,AB=AC=10,BC=12,D、E分别为AB,AC中点,F、G为线段BC上两点,且FG=6,则阴影部分面积为24.