题目内容
15.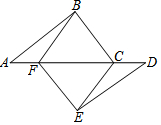 如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.
如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.
分析 首先证明△AFB≌△DCE(SAS),进而得出FB=CE,FB∥CE,进而得出答案.
解答 证明:在△AFB和△DCE中,
$\left\{\begin{array}{l}{AB=DE}\\{∠A=∠D}\\{AF=DC}\end{array}\right.$,
∴△AFB≌△DCE(SAS),
∴FB=CE,∠AFB=∠DCE,
∴∠BFC=∠ECF,
∴FB∥CE,
即FB$\stackrel{∥}{=}$CE,
∴四边形BCEF是平行四边形.
点评 此题主要考查了平行四边形的判定以及全等三角形的判定与性质,得出△AFB≌△DCE是解题关键.

练习册系列答案
相关题目
5.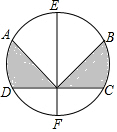 如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )
如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )
 如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )
如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )| A. | 9π | B. | 3π | C. | 6π | D. | $\frac{9}{4}$π |
4.在△PMN中,PM=PN,AB是线段PM的对称轴,且AB分别交线段PM于A,交线段PN于B,若△PMN的周长为60厘米,△BMN的周长为36厘米,则MN的长为( )
| A. | 6厘米 | B. | 12厘米 | C. | 18厘米 | D. | 24厘米 |
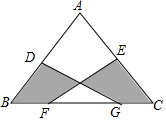 如图,在△ABC中,AB=AC=10,BC=12,D、E分别为AB,AC中点,F、G为线段BC上两点,且FG=6,则阴影部分面积为24.
如图,在△ABC中,AB=AC=10,BC=12,D、E分别为AB,AC中点,F、G为线段BC上两点,且FG=6,则阴影部分面积为24.