题目内容
9.化简:(1)(x-1)2-(x-1)(x+5)
(2)$\frac{2x+2}{x-2}•\frac{{{x^2}-4}}{x+1}$
(3)$\frac{1}{1-x}+\frac{1}{1+x}+\frac{2}{{1+{x^2}}}+\frac{4}{{1+{x^4}}}$.
分析 (1)利用完全平方公式和整式的乘法计算,再进一步合并得出答案即可;
(2)把分子分解因式,进一步约分得出答案即可;
(3)逐步通分得出结果即可.
解答 解:(1)原式=x-2x+1-x-4x+5
=-6x+6;
(2)原式=$\frac{2(x+1)}{x-2}$•$\frac{(x+2)(x-2)}{x+1}$
=2x+4;
(3)原式=$\frac{2}{1-{x}^{2}}$+$\frac{2}{1+{x}^{2}}$+$\frac{4}{1+{x}^{4}}$
=$\frac{4}{1-{x}^{4}}$+$\frac{4}{1+{x}^{4}}$
=$\frac{8}{{1-{x^8}}}$.
点评 此题考查整式的混合运算与分式的混合运算,掌握计算公式和计算方法以及通分约分的方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列二元一次方程组中,以$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$为解的是( )
| A. | $\left\{\begin{array}{l}x-y=1\\ 3x+y=5\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-2y=-3\\ 3x+y=5\end{array}\right.$ | C. | $\left\{\begin{array}{l}x-y=1\\ 3x+y=-5\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=3\\ 3x+y=4\end{array}\right.$ |
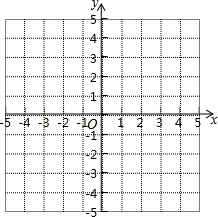 △ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).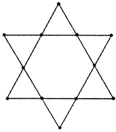 某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你依照举例再设计两种不同的栽树方案(不写作法)
某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你依照举例再设计两种不同的栽树方案(不写作法) 如图,矩形ABCD的对角线AC,BD交于点O,若∠DBC=35°,则∠CAB的度数是55°.
如图,矩形ABCD的对角线AC,BD交于点O,若∠DBC=35°,则∠CAB的度数是55°. 如图,若∠A=∠DCE 则AB∥CD,理由是同位角相等,两直线平行.
如图,若∠A=∠DCE 则AB∥CD,理由是同位角相等,两直线平行.