题目内容
4.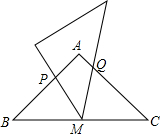 等腰直角三角形ABC中,∠BAC=90°,BC=12,点M为BC中点,含45°的直角三角板的锐角顶点与M重合,当三角板绕点M旋转时,三角板与两直角边交于点P、Q.P、Q分别在AB、AC边上,设BP=x,CQ=y.
等腰直角三角形ABC中,∠BAC=90°,BC=12,点M为BC中点,含45°的直角三角板的锐角顶点与M重合,当三角板绕点M旋转时,三角板与两直角边交于点P、Q.P、Q分别在AB、AC边上,设BP=x,CQ=y.(1)求y与x的函数关系式;
(2)写出x的取值范围.
分析 (1)证明△BPM∽△CMQ,根据相似三角形的对应边的比相等,即可求解;
(2)首先求得AB的长度,则x的范围即可求得.
解答 解:(1)∵M为BC中点,
∴BM=CM=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6.
∵△ABC是等腰直角三角形,
∴∠B=∠C=∠PMQ=45°,
∵△BPM中,∠B+∠BPM+∠BMP=180°,则∠BPM+∠BMP=135°,
又∵∠BMP+∠PMQ+∠QMC=180°,则∠BMP+∠QMC=135°,
∴∠BPM=∠QMC,
又∵∠B=∠C,
∴△BPM∽△CMQ,
∴$\frac{BP}{CM}=\frac{BM}{CQ}$,即$\frac{x}{6}=\frac{6}{y}$,
∴y=$\frac{36}{x}$;
(2)直角△ABC中,AB=BC•sin45°=12×$\frac{\sqrt{2}}{2}$=6$\sqrt{2}$,
则0<x≤6$\sqrt{2}$.
点评 本题考查了相似三角形的判定与性质,证明∠BPM=∠QMC是解题的关键.

练习册系列答案
相关题目
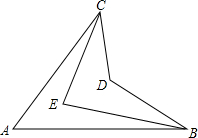 如图,若∠ACE=$\frac{1}{3}$∠ACD,∠ABE=$\frac{1}{3}$∠ABD,猜想∠A,∠CEB和∠CDB之间的数量关系为2∠A+∠CDB=3∠CEB.(写出结论,不必证明)
如图,若∠ACE=$\frac{1}{3}$∠ACD,∠ABE=$\frac{1}{3}$∠ABD,猜想∠A,∠CEB和∠CDB之间的数量关系为2∠A+∠CDB=3∠CEB.(写出结论,不必证明)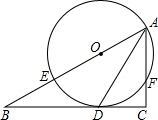 如图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上
如图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上 实数m,n在数轴上对应的点的位置如图所示,则$\sqrt{(m+n)^{2}}$-$\sqrt{{m}^{2}-2mn+{n}^{2}}$等于( )
实数m,n在数轴上对应的点的位置如图所示,则$\sqrt{(m+n)^{2}}$-$\sqrt{{m}^{2}-2mn+{n}^{2}}$等于( ) 如图,在△ABC中,∠A=40°,∠B=78°,CD是∠ACB的角平分线,点E是CD上的点,EF⊥AB,垂足为F,求∠DEF的度数.
如图,在△ABC中,∠A=40°,∠B=78°,CD是∠ACB的角平分线,点E是CD上的点,EF⊥AB,垂足为F,求∠DEF的度数.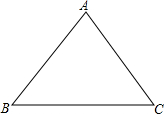 请思考如何利用位似变换的思想,在如图的三角形中作一个等边三角形,使它的三个顶点分别在已知三角形的边上,并且等边三角形的一边与BC平行,即:已知△ABC,求作等边△DEF,使它的三个顶点分别在△ABC的边上,且EF∥BC.
请思考如何利用位似变换的思想,在如图的三角形中作一个等边三角形,使它的三个顶点分别在已知三角形的边上,并且等边三角形的一边与BC平行,即:已知△ABC,求作等边△DEF,使它的三个顶点分别在△ABC的边上,且EF∥BC.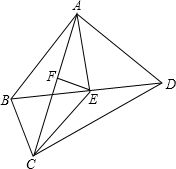 如图,在四边形ABCD中,∠BAD=90°,AB=AD=8,BC=4,E是BD的中点,AE=CE.
如图,在四边形ABCD中,∠BAD=90°,AB=AD=8,BC=4,E是BD的中点,AE=CE.