题目内容
16．
如图，在△ABC中，∠A=40°，∠B=78°，CD是∠ACB的角平分线，点E是CD上的点，EF⊥AB，垂足为F，求∠DEF的度数．
分析 根据三角形的内角和定理得到∠ACB=62°，由角平分线的定义得到∠ACD=$\frac{1}{2}∠$ACB=31°，根据外角的性质得到∠BDC=∠A+∠ACD=71°，即可得到结论．
解答 解：∵在△ABC中，∠A=40°，∠B=78°，
∴∠ACB=62°，
∵CD是∠ACB的角平分线，
∴∠ACD=$\frac{1}{2}∠$ACB=31°，
∴∠BDC=∠A+∠ACD=71°，
∵EF⊥AB，
∴∠DFE=90°，
∴∠DEF=19°．
点评 本题考查了三角形的内角和，三角形的外角的性质，熟练掌握三角形的内角和是解题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
如图，直线AB与CD相交于O，EF⊥AB于F，GH⊥CD于H．求证：EF和GH必相交．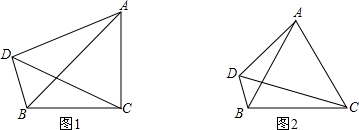
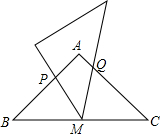等腰直角三角形ABC中，∠BAC=90°，BC=12，点M为BC中点，含45°的直角三角板的锐角顶点与M重合，当三角板绕点M旋转时，三角板与两直角边交于点P、Q．P、Q分别在AB、AC边上，设BP=x，CQ=y．
如图，AB∥CD，AE交DE于点C，DE⊥AE，垂足为E，∠A=41°，求∠D的度数．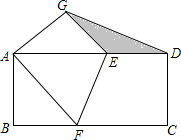
如图，把一张长方形纸片ABCD折叠起来，使其对角顶点A与C重合，D与G重合．若长方形的长BC为8，宽AB为4，求：