题目内容
9. 实数m,n在数轴上对应的点的位置如图所示,则$\sqrt{(m+n)^{2}}$-$\sqrt{{m}^{2}-2mn+{n}^{2}}$等于( )
实数m,n在数轴上对应的点的位置如图所示,则$\sqrt{(m+n)^{2}}$-$\sqrt{{m}^{2}-2mn+{n}^{2}}$等于( )| A. | 0 | B. | 2m | C. | 2n | D. | 2m+2n |
分析 根据二次根式的性质,可得答案.
解答 解:由数轴上的位置,得
m>0>n,且|m|>|n|.
$\sqrt{(m+n)^{2}}$-$\sqrt{{m}^{2}-2mn+{n}^{2}}$=|m+n|-|m-n|=m+n-(m-n)=2n.
故选:C.
点评 本题考查了二次根式的性质与化简,利用二次根式的性质$\sqrt{{a}^{2}}$=a (a≥0).

练习册系列答案
相关题目
19.把-(x-y)-z去括号得( )
| A. | -x+y-z | B. | -x-y-z | C. | -x+y+z | D. | -x-y+z |
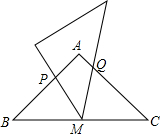 等腰直角三角形ABC中,∠BAC=90°,BC=12,点M为BC中点,含45°的直角三角板的锐角顶点与M重合,当三角板绕点M旋转时,三角板与两直角边交于点P、Q.P、Q分别在AB、AC边上,设BP=x,CQ=y.
等腰直角三角形ABC中,∠BAC=90°,BC=12,点M为BC中点,含45°的直角三角板的锐角顶点与M重合,当三角板绕点M旋转时,三角板与两直角边交于点P、Q.P、Q分别在AB、AC边上,设BP=x,CQ=y. 如图,AB∥CD,AE交DE于点C,DE⊥AE,垂足为E,∠A=41°,求∠D的度数.
如图,AB∥CD,AE交DE于点C,DE⊥AE,垂足为E,∠A=41°,求∠D的度数.