题目内容
15．
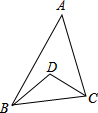如图，在△ABC中，∠A=40°，D点是∠ABC和∠ACB角平分线的交点，则∠BDC=110°．
分析 由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70°，再利用三角形内角和定理即可求出∠BDC的度数．
解答 解：∵D点是∠ABC和∠ACB角平分线的交点，
∴∠CBD=∠ABD=$\frac{1}{2}$∠ABC，∠BCD=∠ACD=$\frac{1}{2}$∠ACB，
∴∠ABC+∠ACB=180°-40°=140°，
∴∠DBC+∠DCB=70°，
∴∠BDC=180°-70°=110°，
故答案为：110°．
点评 此题主要考查学生对角平分线性质，三角形内角和定理，熟记三角形内角和定理是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
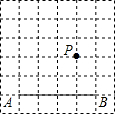如图，在方格纸中，点A，B，P都在格点上．请按要求画出以AB为边的格点四边形，使P在四边形内部（不包括边界上），且P到四边形的两个顶点的距离相等．
端午节期间，某商场为了吸引顾客，设立了一个可以自由转动的转盘（转盘被平均分成16份），并规定：顾客每购买100元的商品，就能获得一次转转盘的机会，如果转盘停止后，指针正好对准红色、黄色或绿色区域，顾客就可以分别获得玩具熊、童话书、水彩笔．小明和妈妈购买了125元的商品，请你分析计算：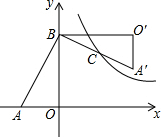
如图，在Rt△AOB中，两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，将△AOB绕点B逆时针旋转90°后得到△A′O′B．若反比例函数$y=\frac{k}{x}$的图象恰好经过斜边A′B的中点C，S△ABO=4，tan∠BAO=2，则k的值为（ ）