题目内容
3．如图，在平面直角坐标系xOy中，过点A（-6，0）的直线l1与直线l2：y=2x相交于点B（m，4）．
（1）求直线l1的表达式；
（2）过动点P（n，0）且垂于x轴的直线与l1，l2的交点分别为C，D，当点C位于点D上方时，写出n的取值范围．
分析 （1）先求出点B坐标，再利用待定系数法即可解决问题．
（2）由图象可知直线l1在直线l2上方即可，由此即可写出n的范围．
解答 解：（1）∵点B在直线l2上，
∴4=2m，
∴m=2，点B（2，4）
设直线l1的表达式为y=kx+b，
由题意$\left\{\begin{array}{l}{2k+b=4}\\{-6k+b=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=3}\end{array}\right.$，
∴直线l1的表达式为y=$\frac{1}{2}$x+3．
（2）由图象可知n＜2．
点评 本题考查两条直线平行、相交问题，解题的关键是灵活应用待定系数法，学会利用图象根据条件确定自变量取值范围．
练习册系列答案
一本好题口算题卡系列答案
相关题目
13．
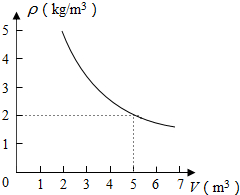在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度ρ（单位：kg/m3）是体积V（单位：m3）的反比例函数，它的图象如图所示，当V=10m3时，气体的密度是（ ）
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度ρ（单位：kg/m3）是体积V（单位：m3）的反比例函数，它的图象如图所示，当V=10m3时，气体的密度是（ ）| A． | 1kg/m3 | B． | 2kg/m3 | C． | 100kg/m3 | D． | 5kg/m3 |
14．2015年全国两会民生话题成为社会焦点，临沂市记者为了了解百胜“两会民生话题”的聚集点，随机调查了临沂市部分市民，并对调查结果进行了整理，绘制了如图所示的不完整的统计图表．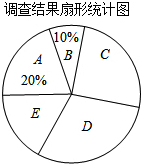
请根据图表中提供的信息解答下列问题：
（1）填空：m=40，n=100．扇形统计图中E组所占的百分比为15%；
（2）临沂市现有人口大约1100万人，请你估计其中关注D组话题的市民人数；
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？
| 组别 | 焦点话题 | 频数（人数） |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
（1）填空：m=40，n=100．扇形统计图中E组所占的百分比为15%；
（2）临沂市现有人口大约1100万人，请你估计其中关注D组话题的市民人数；
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？
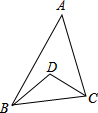如图，在△ABC中，∠A=40°，D点是∠ABC和∠ACB角平分线的交点，则∠BDC=110°．