题目内容
12.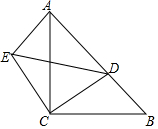 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点,若AB=14,BD=6,将△BCD绕点C逆时针方向旋转到△ACE的位置,对于下列说法:①△ADE是直角三角形,②△CDE是等腰三角形,③DE=10,④CD=5$\sqrt{2}$.其中正确说法是①②③④(填序号).
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点D为斜边AB上一点,若AB=14,BD=6,将△BCD绕点C逆时针方向旋转到△ACE的位置,对于下列说法:①△ADE是直角三角形,②△CDE是等腰三角形,③DE=10,④CD=5$\sqrt{2}$.其中正确说法是①②③④(填序号).
分析 先依据等腰直角三角形的性质得到∠B=∠BAC=45°,然后依据旋转的性质可得到△BCD≌△ACE,然后找出相等的线段和相等的角,最后,再依据勾股定理、等腰三角形的性质和判定进行解答即可.
解答 解:∵AC=BC,∠ACB=90°,
∴∠ABC=∠BAC=45°.
由旋转的性质可知∠EAC=∠B=45°,
∴∠EAD=90°,故①正确.
∵∠C=90°,
∴∠ACD+∠BCD=90°.
由旋转的性质可知:∠DCB=∠ACE,CE=CD,
∴∠ECD=90°.
∴△CDE是等腰三角形,故②正确.
∵AB=14,BD=6,
∴AD=8.
由旋转的性质可知AE=BD=6,
∴在Rt△ADE中,DE=$\sqrt{A{E}^{2}+A{D}^{2}}$=10,故③正确.
∵△ECD为等腰直角三角形,ED=10,
∴CD=5$\sqrt{2}$.
答案:①②③④.
点评 本题主要考查的是旋转的性质、等腰直角三角形的性质和判定、勾股定理的应用,熟练掌握相关知识是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.一次函数y=kx-k(k≠0),若y随x的增大而减小,则该函数的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠AOB1=130°.
如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠AOB1=130°.
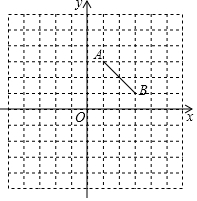 线段AB在直角坐标系中的位置如图.
线段AB在直角坐标系中的位置如图.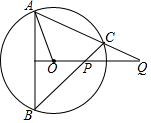 如图,AB为圆O的弦,QO⊥AB,QA交⊙O于C,BC交QO于P,求证:OA2=OP•OQ.
如图,AB为圆O的弦,QO⊥AB,QA交⊙O于C,BC交QO于P,求证:OA2=OP•OQ.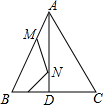 等边△ABC的边长是8,AD⊥BC,E是BD的中点,M、N分别是AB、AD上的动点,求MN+EN的最小值.
等边△ABC的边长是8,AD⊥BC,E是BD的中点,M、N分别是AB、AD上的动点,求MN+EN的最小值.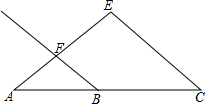 如图所示,点B为△AEC的边AC上一点(点B不与点A、C重合),连接EB,射钱BF∥EC交AE于点F,过点A作∠EAD=∠BEA,交线段BF的延长线于点D.
如图所示,点B为△AEC的边AC上一点(点B不与点A、C重合),连接EB,射钱BF∥EC交AE于点F,过点A作∠EAD=∠BEA,交线段BF的延长线于点D.