题目内容
11.已知关于x的函数y=x2+2ax+2在-5≤x≤5上.(1)当a=-1时,求函数的最大值和最小值;
(2)当a为实数时,求函数的最大值.
分析 (1)将a=-1代入得到抛物线的解析式,求得抛物线的对称轴和顶点坐标,根据x的范围和抛物线的对称性可确定出最大值和最小值;
(2)先利用配方法求得抛物线的对称轴和顶点的纵坐标,然后根据对称轴的位置以及抛物线的对称性确定出最大值和最小值.
解答 解:(1)当a=-1时,y=x2-2x+2=(x-1)2+1,
当x=1时,有最小值y=1;当x=-5时,有最大值y=37;
(2)y=x2+2ax+2=(x+a)2+2-a2.抛物线的对称轴为x=-a.
①当-a≤-5即a≥5时,当x=-5时取最小值,y=27-10a,在x=5时取最大值为y=27+10a;
②当-5<a≤0时,即0≤a≤5时,顶点处取最小值,最小值为y=2-a2,当x=5时,有最大值,最大值为y=27+10a;
③当0≤-a<5时,即-5<a<0时,即-5<a<0,顶点处取最小值,y=2-a2,当x=-5时,有最大值为y=27-10a;
④当-a≥5即a≤-5时,当x=5时,最小值为y=27+10a,当x=-5时,最大值为y=27-10a.
点评 本题主要考查的是二次函数的最值,掌握根据对称轴所在的位置结合自变量x的范围确定出最大值和最小值是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
1.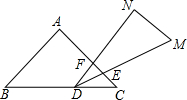 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )| A. | 105° | B. | 115° | C. | 120° | D. | 135° |
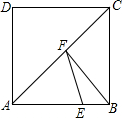 如图,在边长为4的长方形ABCD中,E是AB边上一点,且AE=3,点F为对角线AC上的动点,则△BEF周长的最小值为( )
如图,在边长为4的长方形ABCD中,E是AB边上一点,且AE=3,点F为对角线AC上的动点,则△BEF周长的最小值为( ) 如图,由A到B的方向是东偏南30°.
如图,由A到B的方向是东偏南30°.