题目内容
1．
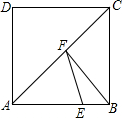如图，在边长为4的长方形ABCD中，E是AB边上一点，且AE=3，点F为对角线AC上的动点，则△BEF周长的最小值为（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
分析 连接BD，DE，根据正方形的性质可知点B与点D关于直线AC对称，故DE的长即为BF+FE的最小值，进而可得出结论．
解答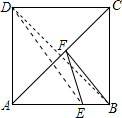 
解：连接BD，DE，
∵四边形ABCD是正方形，
∴点B与点D关于直线AC对称，
∴DE的长即为BF+EF的最小值，
∵DE=BF+EF=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5，
∴△BEF周长的最小值=DE+BE=5+1=6．
故选B．
点评 本题考查的是轴对称-最短路线问题，熟知轴对称的性质是解答此题的关键．
练习册系列答案
相关题目
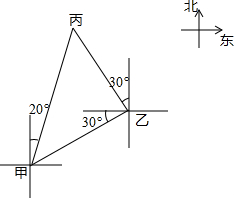如图所示，有甲、乙、丙三个村庄，已知丙村在乙村北偏西30°方向，丙村在甲村北偏东20°方向，甲村在乙村西偏南30°方向，现要从甲村分别向乙村、丙村各修一条公路，则这两条公路应成多少度角？