题目内容
16.求方程x2+3x-1=0的解,除了用课本的方法外,也可以采用图象的方法:画出直线y=x+3和双曲线y=$\frac{1}{x}$的图象,则两图象交点的横坐标即为该方程的解.类似地,可以判断方程x3+x-1=0的解的个数有1个.分析 根据题意断方程x3+x-1=0的解的个数可以转化为确定y=x2+1和y=$\frac{1}{x}$的交点坐标即可.
解答 解:由x3+x-1=0得:x3+x=1,
方程两边同时除以x得:x2+1=$\frac{1}{x}$,
在同一坐标系中作出y=x2+1和y=$\frac{1}{x}$的图象为: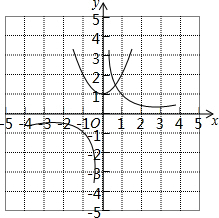
观察图象有一个交点,
∴可以判断方程x3+x-1=0的解的个数有1个,
故答案为:1.
点评 本题考查了反比例函数的图象和二次函数的图象,解题的关键是将方程转化为求图象的交点情况.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
7.在一次有24000名学生参加的数学质量抽测的成绩中,随机取2000名考生的数学成绩进行分析,则在该抽样中,样本指的是( )
| A. | 所抽取的2000名考生的数学成绩 | B. | 24000名考生的数学成绩 | ||
| C. | 2000 | D. | 2000名考生 |
1.函数y=$\frac{1}{x-2}$中,自变量x的取值范围是( )
| A. | x≥2 | B. | x≠2 | C. | x>2 | D. | x≤2 |

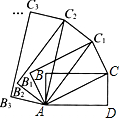 如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn-1的面积为$\frac{{5}^{n}}{{2}^{2n-1}}$.
如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn-1的面积为$\frac{{5}^{n}}{{2}^{2n-1}}$.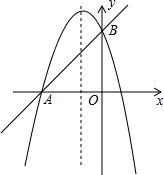 如图,已知抛物线y=-x2+bx+c与直线AB相交于A(-3,0),B(0,3)两点.
如图,已知抛物线y=-x2+bx+c与直线AB相交于A(-3,0),B(0,3)两点.