题目内容
 如图,将四边形纸片ABCD沿EF折叠,点A落在A1处,若∠1+∠2=100°,则∠A的度数是( )
如图,将四边形纸片ABCD沿EF折叠,点A落在A1处,若∠1+∠2=100°,则∠A的度数是( )| A、80° | B、60° |
| C、50° | D、40° |
考点:三角形内角和定理,翻折变换(折叠问题)
专题:
分析:根据翻折变换的性质和平角的定义求出∠3+∠4,再利用三角形的内角和定理列式计算即可得解.
解答: 解:∵四边形纸片ABCD沿EF折叠,点A落在A1处,
解:∵四边形纸片ABCD沿EF折叠,点A落在A1处,
∴∠3+∠4=
(180°-∠1)+
(180°-∠2)=180°-
(∠1+∠2),
∵∠1+∠2=100°,
∴∠3+∠4=180°-
×100°=180°-50°=130°,
在△AEF中,∠A=180°-(∠3+∠4)=180°-130°=50°.
故选C.
 解:∵四边形纸片ABCD沿EF折叠,点A落在A1处,
解:∵四边形纸片ABCD沿EF折叠,点A落在A1处,∴∠3+∠4=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠1+∠2=100°,
∴∠3+∠4=180°-
| 1 |
| 2 |
在△AEF中,∠A=180°-(∠3+∠4)=180°-130°=50°.
故选C.
点评:本题考查了三角形的内角和定理,翻折变换的性质,平角的定义,熟记各性质并整体思想的利用是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 有一种公益叫“光盘”.所谓“光盘”,就是吃光你盘子中的食物,杜绝“舌尖上的浪费”.某校九年级开展“光盘行动”宣传活动,根据各班级参加该活动的总人次折线统计图,下列说法正确的是( )
有一种公益叫“光盘”.所谓“光盘”,就是吃光你盘子中的食物,杜绝“舌尖上的浪费”.某校九年级开展“光盘行动”宣传活动,根据各班级参加该活动的总人次折线统计图,下列说法正确的是( )| A、极差是40 |
| B、中位数是58 |
| C、平均数大于58 |
| D、众数是5 |
把y=
x2-2x+1写成y=a(x-h)2+k的形式是( )
| 1 |
| 2 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
梯形的四条边长分别为6,6,6,12,则这个梯形的面积为( )
A、54
| ||
| B、27 | ||
| C、54 | ||
D、27
|
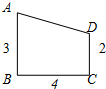 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )| A、10或8 | ||||
B、4
| ||||
C、10或4
| ||||
D、10或2
|
如果代数式
有意义,那么x的取值范围是( )
| ||
| x-2 |
| A、x>3 | B、x≠2 |
| C、x≥3且x≠2 | D、x≥3 |