题目内容
阅读下列材料:
1×2=
(1×2×3-0×1×2),
2×3=
(2×3×4-1×2×3),
3×4=
(3×4×5-2×3×4),
以上三个等式相加,可得:1×2+2×3+3×4=
×3×4×5=20.
读完以上材料,请你计算:1×2+2×3+3×4+…+10×11.
1×2=
| 1 |
| 3 |
2×3=
| 1 |
| 3 |
3×4=
| 1 |
| 3 |
以上三个等式相加,可得:1×2+2×3+3×4=
| 1 |
| 3 |
读完以上材料,请你计算:1×2+2×3+3×4+…+10×11.
考点:规律型:数字的变化类
专题:阅读型
分析:观察不难发现,两个连续的自然数的积等于这两个数与后面的数的积减去与前面的数的积的
,然后列出算式进行计算即可得解.
| 1 |
| 3 |
解答:解:1×2+2×3+3×4+…+10×11,
=
×(1×2×3-0×1×2)+
×(2×3×4-1×2×3)+
×(3×4×5-2×3×4)+…+
×(10×11×12-9×10×11),
=
×(1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+10×11×12-9×10×11),
=
×10×11×12,
=440.
=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
=
| 1 |
| 3 |
=440.
点评:此题考查数字的变化规律,利用类比的思想得出变化规律是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形中,能够折叠成正方体的是( )
A、 |
B、 |
C、 |
D、 |
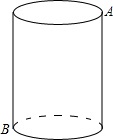 如图,圆柱高12,底面半径3,一只蚂蚁从A点爬到B点去吃食,要爬行的最短路程是
如图,圆柱高12,底面半径3,一只蚂蚁从A点爬到B点去吃食,要爬行的最短路程是 如图,矩形ABCD中,AB=4,BC=2,点B、D在⊙O上,O在AB上,CD交⊙O于E,则CE的长为
如图,矩形ABCD中,AB=4,BC=2,点B、D在⊙O上,O在AB上,CD交⊙O于E,则CE的长为