题目内容
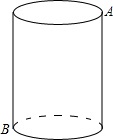如图，圆柱高12，底面半径3，一只蚂蚁从A点爬到B点去吃食，要爬行的最短路程是考点：平面展开-最短路径问题
专题：
分析：要求蚂蚁爬行的最短距离，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果．
解答：
解：将圆柱展开，侧面为矩形，
∵高10，底面⊙O半径为3，
∴BC=π×3=3π，
∴AB=
=
=
=15．
故答案为：15．
解：将圆柱展开，侧面为矩形，∵高10，底面⊙O半径为3，
∴BC=π×3=3π，
∴AB=
| AC2+BC2 |
| 122+(3π)2 |
| 122+92 |
故答案为：15．
点评：此题考查了圆柱的平面展开---最短路径问题，将圆柱展成矩形，求对角线的长即为最短路径．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
小明想将如图所示的一根绳子（无弹性）围成的直角三角形的一个锐角顶点去掉（即把一个锐角顶点变成直角顶点，另两个顶点位置不变）．用这条绳子围成一个长方形，那么所围成的长方形的长、宽各是多少？面积是多少？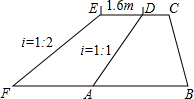
某区为提高某段海堤的防海啸能力，计划修96m长的一堤段（原海堤的横断面如图所示中的梯形ABCD）的堤面加宽1.6m，背水坡比由原来的1：1改为1：2，已知背水坡长AD=8.0m，求完成这一工程所需的土方（要求保留两个有效数字，本题可能使用的数据
下列说法错误的是（ ）
| A、等腰三角形底边上的高所在的直线是对称轴 |
| B、等腰三角形底边上的中线所在的直线是对称轴 |
| C、等腰三角形顶角的平分线所在的直线是对称轴 |
| D、等腰三角形一内角平分线所在的直线是对称轴 |