Question

5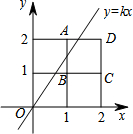．将2×2的正方形网格如图放置在平面直角坐标系中，每个小正方形的顶点称为格点，每个小正方形的边长都是1，正方形ABCD的顶点都在格点上．若直线y=kx（k≠0）与正方形ABCD有公共点，则k的取值范围是（　　）

• A． k≤2
• B． $k≥\frac{1}{2}$
• C． $\frac{1}{2}≤k≤2$
• D． $\frac{1}{2}＜k＜2$

Answer 1

分析 分别确定点A和点C的坐标，代入正比例函数的解析式即可求得k的取值范围．

解答 解：由题意得：点A的坐标为（1，2），点C的坐标为（2，1），
∵当正比例函数经过点A时，k=2，当经过点C时，k=$\frac{1}{2}$，
∴直线y=kx（k≠0）与正方形ABCD有公共点，k的取值范围是$\frac{1}{2}≤k≤2$，
故选C．

点评 本题考查了正比例函数的性质，解题的关键是求得点A和点C的坐标，难度不大．