题目内容
1.在平面直角坐标系xOy中,直线y=-x+3与x轴、y轴分别交于A、B,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标.分析 分两种情况:①如图1,令x=0,则y=3,令y=0,则x=3,得到OA=OB=3,∠BAO=45°,根据DE⊥OA,推出DE=AE,由于四边形COED是正方形,得到OE=DE,等量代换得到OE=AE,即可得到结论;②如图2,由(1)知△OFC,△EFA是等腰直角三角形,由四边形CDEF是正方形,得到EF=CF,于是得到AF=$\sqrt{2}×\sqrt{2}$OF=2OF,求出OA=OF+2OF=3,即可得到结论.
解答  解:分两种情况;
解:分两种情况;
①如图1,令x=0,则y=3,令y=0,则x=3,
∴OA=OB=3,
∴∠BAO=45°,
∵DE⊥OA,
∴DE=AE,
∵四边形COED是正方形,
∴OE=DE,
∴OE=AE,
∴OE=$\frac{1}{2}$OA=$\frac{3}{2}$,
∴E($\frac{3}{2}$,0);
②如图2,由①知△OFC,△EFA是等腰直角三角形,
∴CF=$\sqrt{2}$OF,AF=$\sqrt{2}$EF,
∵四边形CDEF是正方形,
∴EF=CF,
∴AF=$\sqrt{2}×\sqrt{2}$OF=2OF,
∴OA=OF+2OF=3,
∴OF=1,
∴F(1,0).
点评 本题考查了正方形的性质,一次函数图象上点的坐标特征,等腰直角三角形的性质,正确的画出图形是解题的关键.

练习册系列答案
相关题目
6.点A(-1,y1),B(-2,y2)在反比例函数y=$\frac{2}{x}$的图象上,则y1,y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
10.下列运算正确的是( )
| A. | (-a2)•a3=-a6 | B. | a6÷a3=a2 | C. | a2+a3=a5 | D. | (a3)2=a6 |
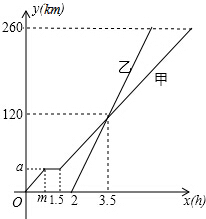 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( ) 如图,在?ABCD中,E、F分别是AB、CD的中点.
如图,在?ABCD中,E、F分别是AB、CD的中点.