题目内容
16.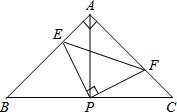 如图,在△ABC中,AB=AC=4,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,现给出以下四个结论:
如图,在△ABC中,AB=AC=4,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,现给出以下四个结论:(1)PE=PF;(2)BE=AF;(3)S四边形AEPF=4;(4)EF=AP;
当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中是正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据等腰直角三角形的性质得:AP⊥BC,AP=$\frac{1}{2}$BC,AP平分∠BAC.所以可证∠C=∠EAP;∠FPC=∠EPA;AP=PC.即证得△APE与△CPF全等.根据全等三角形性质判断结论是否正确.
解答 解:∵AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴AP⊥BC,AP=$\frac{1}{2}$BC=PC,∠BAP=∠CAP=45°=∠C.
∵∠APF+∠FPC=90°,∠APF+∠APE=90°,
∴∠FPC=∠EPA.
在△APE和△CPF中,
$\left\{\begin{array}{l}{∠C=∠BAP}\\{AP=PC}\\{∠EPA=∠FPC}\end{array}\right.$,
∴△APE≌△CPF(ASA).
∴AE=CF,PE=PF,故(1)正确,
∵AB=AC,
∴AB-AE=AC-CF,
即BE=AF,故(2)正确;
∵△APE≌△CPF,
∴S△APE=S△CPF,
∴S四边形AEPF=S△APE+S△APF=S△CPF+S△APF=S△APC=$\frac{1}{2}{S}_{△ABC}$=$\frac{1}{2}×4×4$=4,
故(3)正确;
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=$\frac{1}{2}$BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故(4)错误;
正确的有3个.
故选:C.
点评 此题考查全等三角形的判定和性质,综合性较强,解决本题的关键是证明△APE≌△CPF.

练习册系列答案
相关题目
4.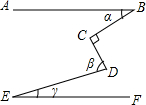 如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
 如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )| A. | ∠β=∠α+∠γ | B. | ∠α+∠β+∠γ=180° | C. | ∠α+∠β-∠γ=90° | D. | ∠β+∠γ-∠α=90° |
1.下列说法正确的是( )
| A. | $\frac{1}{81}$的立方根是$\frac{1}{9}$ | B. | -$\frac{1}{81}$的平方根是$\frac{1}{9}$ | ||
| C. | $\frac{1}{27}$的算术平方根是$\frac{1}{3}$ | D. | -$\frac{1}{27}$的立方根是-$\frac{1}{3}$ |
5.两个连续偶数之积为168,则这两个连续偶数之和为( )
| A. | 26 | B. | -26 | C. | ±26 | D. | 都不对 |
6.下列运算正确的是( )
| A. | x3•x3=2x6 | B. | (x3)2=x6 | C. | (-2x2)2=-4x4 | D. | x5÷x=x5 |
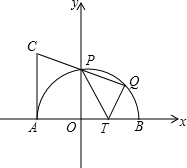 如图,在平面直角坐标系中,半径为2的半圆O与x轴交于A、B两点,与y轴交于点P,T是OB上的一点,OT=a(0<a<2),过A作AC⊥AB,且AC=AT,连接CP并延长交半圆于另一点Q,且Q恰为弧PB中点.
如图,在平面直角坐标系中,半径为2的半圆O与x轴交于A、B两点,与y轴交于点P,T是OB上的一点,OT=a(0<a<2),过A作AC⊥AB,且AC=AT,连接CP并延长交半圆于另一点Q,且Q恰为弧PB中点.