题目内容
9．
如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A、B、C、D、E的坐标分别是（0，a）、（-3，2）、（b，m）、（-b，m），则点E的坐标是（ ）| A． | （2，-3） | B． | （2，3） | C． | （3，2） | D． | （3，-2） |
分析 根据题意得出y轴位置，进而利用正多边形的性质得出E点坐标．
解答 解：如图所示：
∵A（0，a），
∴点A在y轴上，
∵C，D的坐标分别是（b，m），（c，m），
∴B，E点关于y轴对称，
∵B的坐标是：（-3，2），
∴点E的坐标是：（3，2）．
故选：C．
点评 此题主要考查了坐标与图形的性质，正确得出y轴的位置是解题关键．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
19．
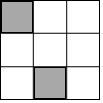如图，在3×3的正方形网格中，已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，能使三个被涂黑的小正方形组成一个轴对称图形的概率是（ ）
如图，在3×3的正方形网格中，已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，能使三个被涂黑的小正方形组成一个轴对称图形的概率是（ ）| A． | $\frac{5}{7}$ | B． | $\frac{4}{7}$ | C． | $\frac{3}{7}$ | D． | $\frac{2}{7}$ |
20．-$\frac{1}{5}$相反数的倒数是（ ）
| A． | $-\frac{1}{5}$ | B． | $\frac{1}{5}$ | C． | 5 | D． | -5 |
17．
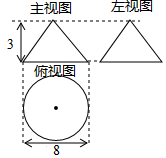已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积是（ ）
已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积是（ ）| A． | 40π | B． | 24π | C． | 20 π | D． | 12π |
4．
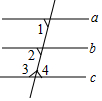如图，下列推理错误的是（ ）
如图，下列推理错误的是（ ）| A． | ∵∠1=∠2，∴a∥b | B． | ∵b∥c，∴∠2=∠4 | ||
| C． | ∵a∥b，b∥c，∴a∥c | D． | ∵∠2+∠3=180°，∴a∥c |
14．估计$\sqrt{5}$+1的值在（ ）
| A． | 1和2之间 | B． | 2和3之间 | C． | 3和4之间 | D． | 4和5之间 |
1．4cos60°的值为（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{\sqrt{3}}{2}$ | D． | 2$\sqrt{3}$ |
18．两名同学都进行了5次立定跳远测试．经计算，他们的平均成绩相同，若要比较这两名同学的成绩谁更稳定，通常还需要比较他们成绩的（ ）
| A． | 众数 | B． | 中位数 | C． | 方差 | D． | 以上都不对 |
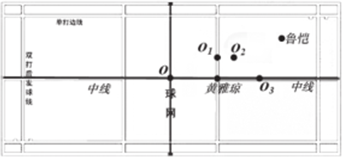2017 全英羽毛球公开赛混双决赛，中国组合鲁恺/黄雅琼，对阵马来西亚里约奥运亚军陈炳顺/吴柳萤，鲁恺/黄雅琼两名小将的完美配合结果获胜．如图是羽毛球场地示意图，x 轴平行场地的中线，y 轴平行场地的球网线，设定鲁恺的坐标是（3，1），黄雅琼的坐标是（0，-1），则坐标原点为（ ）