题目内容
16.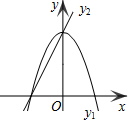 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越小; ③使得M大于2的x值不存在;④使得M=1的x值是-$\frac{1}{2}$或$\frac{\sqrt{2}}{2}$.
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 观察图象,当x>0,一次函数图象在二次函数图象的上方,则可对①进行判断;利用一次函数和二次函数的增减性可对②进行判断;利用二次函数的最值和M的意义可对③进行判断;分别解-2x2+2=1和2x+2=1,再计算出对应的M的值,从而可对④进行判断.
解答 解:当x>0时,y1<y2,所以①错误;
当x<0时,y1、y2都随x的增大而增大,则x值越大,M值越大,所以②错误;
因为抛物线y1=-2x2+2有最大值为2,所以y1、y2中的较小值M不可能大于2,所以③正确;
若-2x2+2=1,解得x=±$\frac{\sqrt{2}}{2}$,当x=$\frac{\sqrt{2}}{2}$时,M=1;若2x+2=1,解得x=-$\frac{1}{2}$,此时M=1,所以④正确.
故选B.
点评 本题考查了二次函数与不等式(组):对于二次函数y=ax2+bx+c(a、b、c是常数,a≠0)与不等式的关系,一般要转化成关于x的不等式,解不等式求得自变量x的取值范围.或利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,可作图利用交点直观求解,也可把两个函数解析式列成不等式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.为了解某市参加中考的45000名学生的身高情况,抽查了其中1500名学生的身高进行统计分析.下面叙述正确的是( )
| A. | 45000名学生是总体 | |
| B. | 1500名学生的身高是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 以上调查是全面调查 |
4.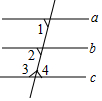 如图,下列推理错误的是( )
如图,下列推理错误的是( )
 如图,下列推理错误的是( )
如图,下列推理错误的是( )| A. | ∵∠1=∠2,∴a∥b | B. | ∵b∥c,∴∠2=∠4 | ||
| C. | ∵a∥b,b∥c,∴a∥c | D. | ∵∠2+∠3=180°,∴a∥c |
11.在下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.4cos60°的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |
8. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
5.在-2.5,$\frac{1}{3}$,0,2这四个数中,最小的数是( )
| A. | -2.5 | B. | $\frac{1}{3}$ | C. | 0 | D. | 2 |