题目内容
19.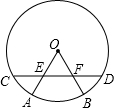 如图,CD是⊙O的弦,$\widehat{AC}$=$\widehat{BD}$,OA,OB分别交CD于点E,F.判断△OEF的形状,并说明理由.
如图,CD是⊙O的弦,$\widehat{AC}$=$\widehat{BD}$,OA,OB分别交CD于点E,F.判断△OEF的形状,并说明理由.
分析 连结OC,OD,根据等腰三角形的性质可知∠OAE=∠ODF,再由$\widehat{AC}$=$\widehat{BD}$可知∠COE=∠DOF,根据ASA定理得出△COE≌△DOF,故可得出OE=OF,由此可得出结论.
解答 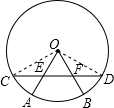 解:△OEF是等腰三角形.
解:△OEF是等腰三角形.
理由:连接OC,OD,
∵OC=OD,
∴∠OCE=∠ODF.
∵$\widehat{AC}$=$\widehat{BD}$,
∴∠COE=∠DOF.
在△COE与△DOF中,
$\left\{\begin{array}{l}∠COE=∠DOE\\ OC=OD\\∠COE=∠DOF\end{array}\right.$,
∴△COE≌△DOF(ASA),
∴OE=OF,
∴△OEF是等腰三角形.
点评 本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.

练习册系列答案
相关题目
 有理数a,b,c在数轴上的位置如图所示,化简|a+c|-|a-b-c|+2|b-a|-|b+c|.
有理数a,b,c在数轴上的位置如图所示,化简|a+c|-|a-b-c|+2|b-a|-|b+c|. 如图,∠1=∠2,∠3=∠4,点B,D,C,F在一条直线上,EF⊥AD于E,
如图,∠1=∠2,∠3=∠4,点B,D,C,F在一条直线上,EF⊥AD于E,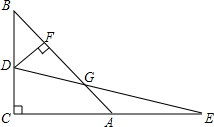 如图,在等腰Rt△ABC中,∠C=90°,动点D从点B出发沿BC方向匀速运动,同时动点E从点A出发沿射线CA方向以相同的速度匀速运动,当点D到达点C时,当点C到达C时,D,E同时停止运动,过点D作DF⊥AB于点F,连接DE交AB于点G,在整个运动过程中(不计点D与B,C重合的情形),线段FG的长度变化情况是( )
如图,在等腰Rt△ABC中,∠C=90°,动点D从点B出发沿BC方向匀速运动,同时动点E从点A出发沿射线CA方向以相同的速度匀速运动,当点D到达点C时,当点C到达C时,D,E同时停止运动,过点D作DF⊥AB于点F,连接DE交AB于点G,在整个运动过程中(不计点D与B,C重合的情形),线段FG的长度变化情况是( )