题目内容
4. 如图,∠1=∠2,∠3=∠4,点B,D,C,F在一条直线上,EF⊥AD于E,
如图,∠1=∠2,∠3=∠4,点B,D,C,F在一条直线上,EF⊥AD于E,(1)求证:∠ADF=∠DAF;
(2)求证:AE=DE.
分析 (1)由∠ADF=是△ABD的外角,可得∠ADF=∠1+∠4,又由∠DAF=∠2+∠3,易证得:∠ADF=∠DAF;
(2)由∠ADF=∠DAF,可证得AF=DF,然后由EF⊥AD,根据等腰三角形三线合一的性质证得结论.
解答 证明:(1)∵∠ADF=是△ABD的外角,
∴∠ADF=∠1+∠4,
∵∠DAF=∠2+∠3,∠1=∠2,∠3=∠4,
∴∠ADF=∠DAF;
(2)∵∠ADF=∠DAF,
∴AF=DF,
∵EF⊥AD,
∴AE=DE.
点评 此题考查了等腰三角形的判定与性质.注意证得△ADF是等腰三角形是关键.

练习册系列答案
相关题目
16.下列各组式子中,同类项有( )
①-5x2y2与$\frac{2}{3}$x2y2;②42与-10;③3a2b与-4a2bc;④23a2与-3a2b2;⑤3p2q与-qp2.
①-5x2y2与$\frac{2}{3}$x2y2;②42与-10;③3a2b与-4a2bc;④23a2与-3a2b2;⑤3p2q与-qp2.
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
13.关于x的方程x-2a=0的解比关于y的方程3y-a=0的解大5,则a的值是( )
| A. | 6 | B. | -6 | C. | 3 | D. | -3 |
14.下列命题中,是真命题的是( )
| A. | 圆的半径都相等 | |
| B. | 如果两条弧的长都是8cm,那么这两条弧是等弧 | |
| C. | 圆心是直径的中点 | |
| D. | 到一个圆的圆心距离相等的点不一定在这个圆上 |
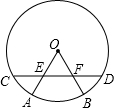 如图,CD是⊙O的弦,$\widehat{AC}$=$\widehat{BD}$,OA,OB分别交CD于点E,F.判断△OEF的形状,并说明理由.
如图,CD是⊙O的弦,$\widehat{AC}$=$\widehat{BD}$,OA,OB分别交CD于点E,F.判断△OEF的形状,并说明理由.